Confidence Interval For Population Variance Calculator
Use below Confidence interval for population variance calculator to calculate degees of freedom,chi-square critical values, confidence limits based on input sample size,sample standard deviation and confidence interval (90%,95%,98% or 99%)
Confidence Interval for Variance Calculator
| Confidence Interval for Variance Calculator | |
|---|---|
| Sample Size ($n$) | |
| Sample Standard Deviation ($s$) | |
| Confidence Level ($1-\alpha$) | |
| Confidence Interval for Variance Calculator Results | |
| Degrees of Freedom : (df) | |
| Chi-square critical value 1: | |
| Chi-square critical value 2: | |
| Lower Confidence Limits: | |
| Upper Confidence Limits: | |
How to use Confidence Interval for Variance Calculator?
Step 1 - Enter the Sample Size (n)
Step 2 - Enter the Sample Standard Deviation (s)
Step 3 - Select Confidence level (90%,95%,98% or 99%)
Step 4 - Click on “Calculate” button to calculate Confidence Interval for variance
Step 5 - Calculate Degrees of Freedom (df)
Step 6 - Calculate Chi-Square critical value 1
Step 7 - Calculate Chi-Square critical value 2
Step 8 - Calculate lower confidence limits
Step 9 - Calculate upper confidence limits
Confidence Interval for Variance Formula
Let $X_1, X_2, \cdots , X_n$ be a random sample of size $n$ from $N(\mu, \sigma^2)$.
Formula
$100(1-\alpha)$% confidence interval estimate of population variance $\sigma^2$ is
$\bigg(\dfrac{(n-1)s^2}{\chi^2_{(\alpha/2,n-1)}}, \dfrac{(n-1)s^2}{\chi^2_{(1-\alpha/2,n-1)}}\bigg)$
where,
$\overline{X}=\frac{1}{n} \sum X_i$is the sample mean,$s^2= \frac{1}{n-1}\sum (X_i-\overline{X})^2$is the sample variance,$1-\alpha$is the confidence coefficient,$\chi^2_{(1-\alpha/2,n-1)}$and$\chi^2_{(1-\alpha/2,n-1)}$are the table values of$\chi^2$.
Confidence Interval for Variance Theory
Let $X_1, X_2, \cdots , X_n$ be a random sample of size $n$ from $N(\mu, \sigma^2)$.
Let $\overline{X}=\frac{1}{n} \sum X_i$ be the sample mean and $s^2=\dfrac{1}{n-1}\bigg(\sum_{i=1}^nx_i^2-\dfrac{\big(\sum x_i\big)^2}{n}\bigg)$ be the sample variance.
Let $C=1-\alpha$ be the confidence coefficient.
We wish to construct a $100(1-\alpha)$% confidence interval of a population variance $\sigma^2$.
$100(1-\alpha)$% confidence interval estimate of population variance $\sigma^2$ is
$$ \begin{aligned} \bigg(\frac{(n-1)s^2}{\chi^2_{(\alpha/2,n-1)}}, \frac{(n-1)s^2}{\chi^2_{(1-\alpha/2,n-1)}}\bigg) \end{aligned} $$
$100(1-\alpha)$% confidence interval estimate of population standard deviation $\sigma^2$ is
$$ \begin{aligned} \sqrt{\bigg(\frac{(n-1)s^2}{\chi^2_{(\alpha/2,n-1)}}}, \sqrt{\frac{(n-1)s^2}{\chi^2_{(1-\alpha/2,n-1)}}}\bigg) \end{aligned} $$
Assumptions
a. The sample is a simple random sample.
b. The population has a normal distribution.
Step by Step procedure
Step by step procedure to estimate confidence interval for population variance $\sigma^2$ is as follows:
Step 1 Specify the confidence level $(1-\alpha)$
Step 2 Given information
Specify the given information, sample size $n$, sample mean $\overline{X}$ and sample variance $s^2$.
Step 3 Specify the formula
$100(1-\alpha)$% confidence interval estimate of population variance $\sigma^2$ is
$$ \begin{aligned} \bigg(\frac{(n-1)s^2}{\chi^2_{(\alpha/2,n-1)}}, \frac{(n-1)s^2}{\chi^2_{(1-\alpha/2,n-1)}}\bigg) \end{aligned} $$
Step 4 Determine the critical value
Determine the critical values $\chi^2_L = \chi^2_{(\alpha/2,n-1)}$ and $\chi^2_R = \chi^2_{(1-\alpha/2,n-1)}$ from $\chi^2$ chi squared statistical table that corresponds to the desired confidence level and the degrees of freedom.
Step 5 Determine the confidence interval
$100(1-\alpha)$% confidence interval estimate for population variance $\sigma^2$ is
$$ \begin{aligned} \bigg(\frac{(n-1)s^2}{\chi^2_{(\alpha/2,n-1)}}, \frac{(n-1)s^2}{\chi^2_{(1-\alpha/2,n-1)}}\bigg) \end{aligned} $$
Confidence Interval for Variance Examples
In this tutorial we will discuss some numerical examples to understand how to construct a confidence interval for population variance or population standard deviation.
Example 1 - Confidence Interval for Variance Calculator
The mean replacement time for a random sample of 12 microwaves is 8.6 years with a standard deviation of 3.6 years. Construct a 95% confidence interval for the population standard deviation.
Solution
Here the sample size is $n=27$, sample standard deviation is $s=6.8$.
We wish to construct a $95$% confidence interval for population standard deviation $\sigma$.
Step 1 Specify the confidence level $(1-\alpha)$
Confidence level is $1-\alpha = 0.95$. Thus, the level of significance is $\alpha = 0.05$.
Step 2 Given information
Given that sample size $n=27$ and sample standard deviation $s =6.8$.
Step 3 Specify the confidence interval for variance formula
$100(1-\alpha)$% confidence interval estimate of population standard deviation $\sigma$ is
$$ \begin{aligned} \bigg(\sqrt{\frac{(n-1)s^2}{\chi^2_{(\alpha/2,n-1)}}}, \sqrt{\frac{(n-1)s^2}{\chi^2_{(1-\alpha/2,n-1)}}}\bigg) \end{aligned} $$
where $\chi^2_{(\alpha/2,n-1)}$ and $\chi^2_{(1-\alpha/2,n-1)}$ are the critical values from $\chi^2$ chi squared distribution with $\alpha$ level of significance and $n-1$ degrees of freedom.
Step 4 Determine the chi-squared confidence interval critical value
The critical values of $\chi^2$ (chi squared) for $\alpha$ level of significance and $n-1$ degrees of freedom are
$\chi^2_{(\alpha/2,n-1)}=\chi^2_{(0.025,26)}=41.923$
and
$\chi^2_{(1-\alpha/2,n-1)}=\chi^2_{(0.975,26)}=13.844$.
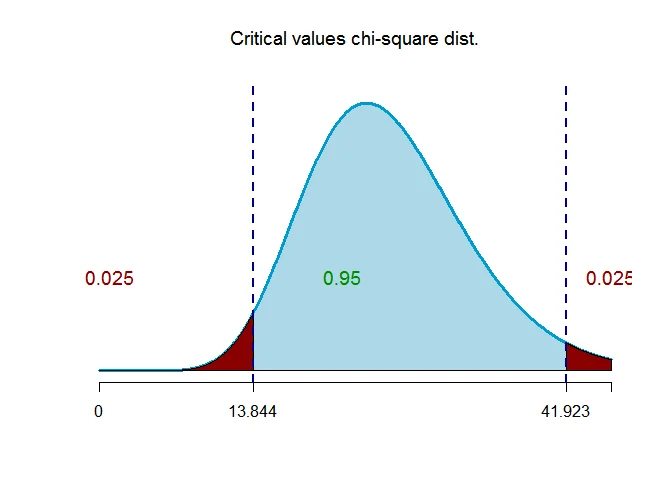
Step 5 Determine the confidence interval
$95$% confidence interval estimate for population standard deviation is
$$ \begin{aligned} \sqrt{\frac{(n-1)s^2}{\chi^2_{(\alpha/2,n-1)}}} &\leq \sigma \leq \sqrt{\frac{(n-1)s^2}{\chi^2_{(1-\alpha/2,n-1)}}}\\ \sqrt{\frac{26*46.24}{41.923}} &\leq \sigma \leq \sqrt{\frac{26*46.24}{13.844}}\\ 5.355 &\leq \sigma \leq 9.319. \end{aligned} $$
Thus 95 percent confidence interval for population standard deviation is $(5.355,9.319)$.
We can be 95 percent confident that the population standard deviation for the replacement time is between $5.355$ and $9.319$.
Example 2 - 99 percent Confidence Interval for Variance Calculator
The percentage rates of home ownership for 8 randomly selected states are listed below.
Estimate the population variance and standard deviation for the percentage rate of home ownership with 99% confidence.
66.0, 75.8, 70.9, 73.9, 63.4, 68.5, 73.3, 65.9.
Solution
Given that the sample size is $n=8$. The sample variance is given by
$$ \begin{aligned} s^2&=\frac{1}{n-1}\bigg(\sum_{i=1}^nx_i^2-\frac{\big(\sum x_i\big)^2}{n}\bigg)\\ &=\frac{1}{8-1}\bigg(39017.17-\frac{\big(557.7\big)^2}{8}\bigg)\\ &=\frac{1}{7}\bigg(39017.17-\frac{311029.29}{8}\bigg)\\ &=\frac{1}{7}\big(138.5087\big)\\ &=19.787 \end{aligned} $$
and sample standard deviation is $s=\sqrt{19.787}=4.4483$.
We wish to construct a 99 percent confidence interval for population variance $\sigma^2$ and standard deviation $\sigma$.
Step 1 Specify the confidence level $(1-\alpha)$
Confidence level is $1-\alpha = 0.99$. Thus, the level of significance is $\alpha = 0.01$.
Step 2 Given information
Given that sample size $n=8$ and sample variance is $19.787$ and standard deviation $s =4.4483$.
Step 3 Specify the confidence interval for variance formula
$100(1-\alpha)$% confidence interval estimate of population variance $\sigma^2$ is
$$ \begin{aligned} \bigg(\frac{(n-1)s^2}{\chi^2_{(\alpha/2,n-1)}}, \frac{(n-1)s^2}{\chi^2_{(1-\alpha/2,n-1)}}\bigg) \end{aligned} $$
and
$100(1-\alpha)$% confidence interval estimate of population standard deviation $\sigma$ is
$$ \begin{aligned} \bigg(\sqrt{\frac{(n-1)s^2}{\chi^2_{(\alpha/2,n-1)}}}, \sqrt{\frac{(n-1)s^2}{\chi^2_{(1-\alpha/2,n-1)}}}\bigg) \end{aligned} $$
where $\chi^2_{(\alpha/2,n-1)}$ and $\chi^2_{(1-\alpha/2,n-1)}$ are the critical values from $\chi^2$ (chi squared) distribution with $\alpha$ level of significance and $n-1$ degrees of freedom.
Step 4 Determine the chi-squared confidence interval critical value
The critical values of $\chi^2$ for $\alpha$ level of significance and $n-1$ degrees of freedom are
$\chi^2_{(\alpha/2,n-1)}=\chi^2_{(0.005,7)}=20.278$
and
$\chi^2_{(1-\alpha/2,n-1)}=\chi^2_{(0.995,7)}=0.989$.
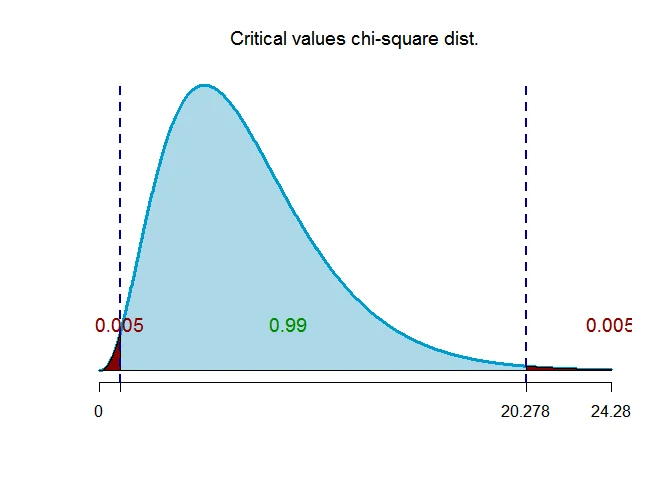
Step 5 Determine the confidence interval
$99$% confidence interval estimate for population variance is
$$ \begin{aligned} \frac{(n-1)s^2}{\chi^2_{(\alpha/2,n-1)}} &\leq \sigma^2 \leq \frac{(n-1)s^2}{\chi^2_{(1-\alpha/2,n-1)}}\\ \frac{7*19.787}{20.278} &\leq \sigma^2 \leq \frac{7*19.787}{0.989}\\ 6.83 &\leq \sigma^2 \leq 140.049. \end{aligned} $$
Thus 99% confidence interval for population variance is $(6.83,140.049)$.
Interpretation
We can be 99 percent confident that the population variance for the percentage rate of home ownership is between $6.8305$ and $140.0495$.
Confidence interval for standard deviation
$99$% confidence interval estimate for population standard deviation is
$$ \begin{aligned} \sqrt{6.83} &\leq \sigma \leq \sqrt{140.049}\\ 2.614 &\leq \sigma \leq 11.834. \end{aligned} $$
Thus $99$% confidence interval for population standard deviation is $(2.614,11.834)$.
Interpretation
We can be $99$% confident that the population standard deviation for the percentage rate of home ownership is between $2.614$ and $11.834$.
Conclusion
Hope you like above article on Confidence Interval for Population Variance Calculator with solved numerical examples.
