Beta Type I Distribution
A continuous random variable $X$ is said to have a beta type I distribution with parameters $\alpha$ and $\beta$ if its p.d.f. is given by
$$ \begin{equation*} f(x)=\left\{ \begin{array}{ll} \frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}, & \hbox{$0\leq x\leq 1$;} \\ 0, & \hbox{Otherwise.} \end{array} \right. \end{equation*} $$
where,
-
$B(\alpha,\beta) =\frac{\Gamma \alpha \Gamma \beta}{\Gamma (\alpha+\beta)}=\int_0^1 x^{\alpha-1}(1-x)^{\beta-1}\; dx$is a beta function and -
$\Gamma \alpha$is a gamma function.
In notation, it can be written as $X\sim \beta_1(\alpha,\beta)$.
Graph of Beta Type I Distribution
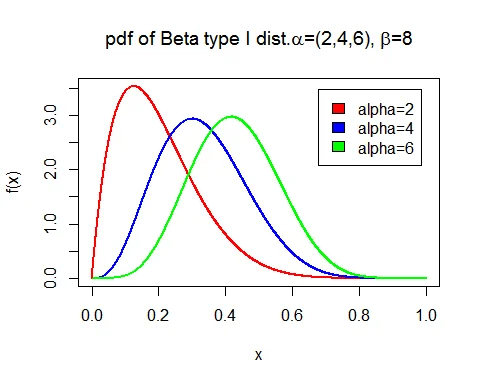
Following graph shows the probability density function of beta type I ditribution with parameters $\alpha=2,4,6$ and $\beta=8$.
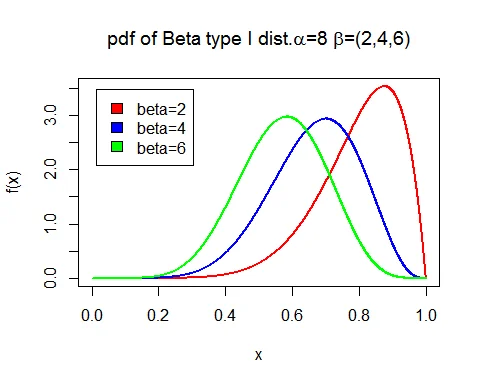
Following graph shows the probability density function of beta type I ditribution with parameters $\alpha=8$ and $\beta=2,4,6$.
Mean of Beta Type I Distribution
The mean of beta type I distribution is $E(X) = \dfrac{\alpha}{\alpha+\beta}$.
Proof
The expected value of beta type I distribution is
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) E(X) &=& \int_{0}^1 x\frac{1}{B(\alpha,\beta)} x^{\alpha-1}(1-x)^{\beta-1}\; dx\\ &=& \frac{1}{B(\alpha,\beta)} \int_{0}^1 x^{\alpha+1-1}(1-x)^{\beta-1}\; dx\\ &=& \frac{1}{B(\alpha,\beta)} B(\alpha+1, \beta)\\ &=& \frac{B(\alpha+1, \beta)}{B(\alpha,\beta)} \\ &=&\frac{\Gamma (\alpha+1) \Gamma \beta}{\Gamma (\alpha+\beta+1)}\cdot \frac{\Gamma(\alpha+\beta)}{\Gamma \alpha \Gamma \beta}\\ &=&\frac{\alpha\Gamma \alpha \Gamma \beta}{(\alpha+\beta)\Gamma (\alpha+\beta)}\cdot \frac{\Gamma(\alpha+\beta)}{\Gamma \alpha \Gamma \beta}\\ &=&\frac{\alpha}{(\alpha+\beta)} \end{eqnarray*} $$
Variance of Beta Type I Distribution
The variance of beta type I distribution is $V(X) = \dfrac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}$.
Proof
The variance of random variable $X$ is given by
$$ \begin{equation*} V(X) = E(X^2) - [E(X)]^2. \end{equation*} $$
Let us find the expected value of $X^2$.
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) E(X^2)&=& \int_{0}^1 x^2\frac{1}{B(\alpha,\beta)} x^{\alpha-1}(1-x)^{\beta-1}\; dx\\ &=& \frac{1}{B(\alpha,\beta)} \int_{0}^1 x^{\alpha+2-1}(1-x)^{\beta-1}\; dx\\ &=& \frac{1}{B(\alpha,\beta)} B(\alpha+2, \beta)\\ &=& \frac{B(\alpha+2, \beta)}{B(\alpha,\beta)} \end{eqnarray*} $$
Using beta function $B(\alpha,\beta) = \dfrac{\Gamma \alpha \Gamma \beta}{\Gamma (\alpha+\beta)}$ and $\Gamma \alpha = (\alpha-1)\Gamma (\alpha-1)$, we have
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) E(X^2) &=&\frac{\Gamma (\alpha+2) \Gamma \beta}{\Gamma (\alpha+\beta+2)}\cdot \frac{\Gamma(\alpha+\beta)}{\Gamma \alpha \Gamma \beta}\\ &=&\frac{(\alpha+1)\alpha\Gamma \alpha \Gamma \beta}{(\alpha+\beta+1)(\alpha+\beta)\Gamma (\alpha+\beta)}\cdot \frac{\Gamma(\alpha+\beta)}{\Gamma \alpha \Gamma \beta}\\ &=&\frac{\alpha(\alpha+1)}{(\alpha+\beta)(\alpha+\beta+1)}. \end{eqnarray*} $$
Thus, variane of $X$ is
$$ \begin{eqnarray*} V(X)&=&E(X^2) - [E(X)]^2\\ &=&\frac{\alpha(\alpha+1)}{(\alpha+\beta)(\alpha+\beta+1)}-\bigg(\frac{\alpha}{(\alpha+\beta)}\bigg)^2\\ &=&\frac{\alpha}{(\alpha+\beta)}\bigg[\frac{\alpha+1}{\alpha+\beta+1}-\frac{\alpha}{\alpha+\beta}\bigg]\\ &=&\frac{\alpha}{(\alpha+\beta)}\bigg[\frac{\alpha^2+\alpha\beta+\alpha+\beta -\alpha^2-\alpha\beta-\alpha}{(\alpha+\beta+1)(\alpha+\beta)}\bigg]\\ &=&\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}. \end{eqnarray*} $$
Harmonic Mean of Beta Type I Distribution
The harmonic mean of beta type I distribution is $H = \dfrac{\alpha-1}{\alpha+\beta-1}$.
Proof
The reciprocal of the harmonic mean of $X$ is
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \frac{1}{HM} &=& E(1/X) \\ &=& \int_{0}^1 \frac{1}{x}\frac{1}{B(\alpha,\beta)} x^{\alpha-1}(1-x)^{\beta-1}\; dx\\ &=& \frac{1}{B(\alpha,\beta)} \int_{0}^1 x^{\alpha-1-1}(1-x)^{\beta-1}\; dx\\ &=& \frac{1}{B(\alpha,\beta)} B(\alpha-1, \beta)\\ &=& \frac{B(\alpha-1, \beta)}{B(\alpha,\beta)} \\ &=&\frac{\Gamma (\alpha-1) \Gamma \beta}{\Gamma (\alpha+\beta-1)}\cdot \frac{\Gamma(\alpha+\beta)}{\Gamma \alpha \Gamma \beta}\\ &=&\frac{\Gamma (\alpha-1) \Gamma \beta}{\Gamma (\alpha+\beta-1)}\cdot \frac{(\alpha+\beta-1)\Gamma(\alpha+\beta-1)}{(\alpha-1)\Gamma (\alpha-1) \Gamma \beta}\\ &=&\frac{\alpha+\beta-1}{\alpha-1}\\ \therefore HM &=& \frac{\alpha-1}{\alpha+\beta-1} \end{eqnarray*} $$
Mode of Beta Type-I distribution
The mode of beta type I distribution is $\dfrac{\alpha-1}{\alpha+\beta-2}$.
Proof
The mode of a beta type I distribution is the value of random variable $X$ at which the density function $f(x)$ becomes maximum.
The p.d.f. of beta type I distribution is
$$ \begin{equation*} f(x)=\left\{ \begin{array}{ll} \frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}, & \hbox{$0\leq x\leq 1$;} \\ 0, & \hbox{Otherwise.} \end{array} \right. \end{equation*} $$
Taking $\log_e$, we get
$$ \begin{equation*} \log_e f(x)=-\log B(\alpha,\beta) +(\alpha-1)\log x+ (\beta-1)\log(1-x). \end{equation*} $$
Differentiating $\log_e f(x)$ w.r.t. $x$, we get
$$ \begin{eqnarray*} \frac{d \log_e f(x)}{dx}& = & 0 +\frac{\alpha-1}{x}+ \frac{\beta-1}{(1-x)}(-1)\\ & = & \frac{\alpha-1}{x}- \frac{\beta-1}{(1-x)}. \end{eqnarray*} $$
By the principal of maxima and minima,
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) & &\frac{d \log_e f(x)}{dx}=0 \\ \Rightarrow & & \frac{\alpha-1}{x}- \frac{\beta-1}{(1-x)}=0\\ \Rightarrow & & (\alpha-1)-x(\alpha-1)= x(\beta-1)\\ \Rightarrow & & x(\alpha+\beta-2) = (\alpha-1)\\ \Rightarrow & & x_0=\frac{\alpha-1}{\alpha+\beta-2}. \end{eqnarray*} $$
Also,
$$ \begin{equation*} \frac{d^2 \log_e f(x)}{dx^2}\bigg|_{x=x_0}< 0. \end{equation*} $$
Hence, the density function $f(x)$ is maximum at $x= x_0 = \dfrac{\alpha-1}{\alpha+\beta-2}$.
Thus, the mode of beta type I distribution is $\dfrac{\alpha-1}{\alpha+\beta-2}$.