Chi-square Test for the Variance
In this tutorial we will discuss a method for testing a claim made about the population variance $\sigma^2$ or population standard deviation $\sigma$. To test the claim about the population variance or population standard deviation we use chi-square test.
In this tutorial we will discuss some numerical examples using six steps approach used in hypothesis testing to test hypothesis about the population variance or population standard deviation.
Example 1
A statistician wishes to test the claim that the standard deviation of the weights of firemen is less than 25 pounds. She selected a random sample of 20 firemen and found $s = 23.2$ pounds. Assuming that the weights of firemen are normally distributed, test the claim of the statistician at the 0.05 level of significance.
Solution
Given that the sample size $n = 20$ and sample standard deviation $s = 23.2$.
Step 1 Hypothesis Problem
The hypothesis testing problem is $H_0 : \sigma = 25$ against $H_1 : \sigma < 25$ ($\text{left-tailed}$).
Step 2 Test Statistic
The test statistic for testing above hypothesis testing problem is
$$ \chi^2 =\frac{(n-1)s^2}{\sigma^2} $$
The test statistic follows a chi-square distribution with $n-1$ degrees of freedom.
Step 3 Level of Significance
The significance level is $\alpha = 0.05$.
Step 4 Critical Value
As the alternative hypothesis is $\text{left-tailed}$, the critical value of $\chi^2$ for $\alpha=0.05$ level of significance and $n-1 = 19$ degrees of freedom $\text{ is }$ $\text{10.117}$ (from $\chi^2$ statistical table).
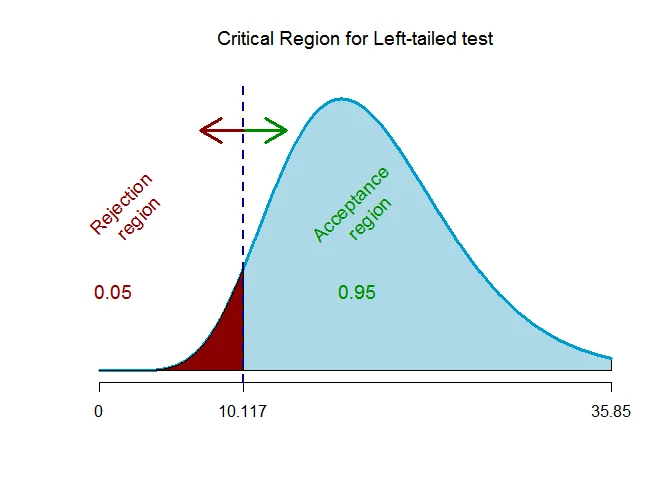
The rejection region (i.e. critical region) is $\chi^2 < 10.117$.
Step 5 Test Statistic
The test statistic under the null hypothesis is
$$ \begin{aligned} \chi^2 &=\frac{(n-1)s^2}{\sigma^2_0}\\ &= \frac{(20-1)*(23.2)^2}{(25)^2}\\ &= 16.362 \end{aligned} $$
Step 6 Decision (Traditional approach)
The test statistic is $\chi^2 =16.362$ which falls $outside$ the critical region, we $\text{fail to reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value Approach)
This is a $\text{left-tailed}$ test, so the p-value is the area to the left of the test statistic ($\chi^2=16.362$) is p-value = $0.367$.
The p-value is $0.367$ which is $\text{greater than}$ the significance level of $\alpha = 0.05$, we $\text{fail to reject}$ the null hypothesis.
Example 2
An engineer is investing the amount of standard deviation in the time it takes a 3D printer to make a particular part. The engineer believes that the standard deviation in the time it takes to make the part is more than 2. Test this at $\alpha = 0.01$ level of significance, using 11 sample times taken while the printer was making these parts. The sample standard deviation is 2.3.
Solution
Given that the sample size $n = 11$ and sample standard deviation $s = 2.3$.
Step 1 Hypothesis Problem
The hypothesis testing problem is $H_0 : \sigma = 2$ against $H_1 : \sigma > 2$ ($\text{right-tailed}$)
Step 2 Test Statistic
The test statistic for testing above hypothesis testing problem is
$$ \chi^2 =\frac{(n-1)s^2}{\sigma^2} $$
The test statistic follows chi-square distribution with $n-1$ degrees of freedom.
Step 3 Level of Significance
The significance level is $\alpha = 0.01$.
Step 4 Critical Value
As the alternative hypothesis is $\text{right-tailed}$, the critical value of $\chi^2$ for $\alpha=0.01$ level of significance and $n-1 = 10$ degrees of freedom $\text{ is }$ $\text{23.209}$ (from $\chi^2$ statistical table).
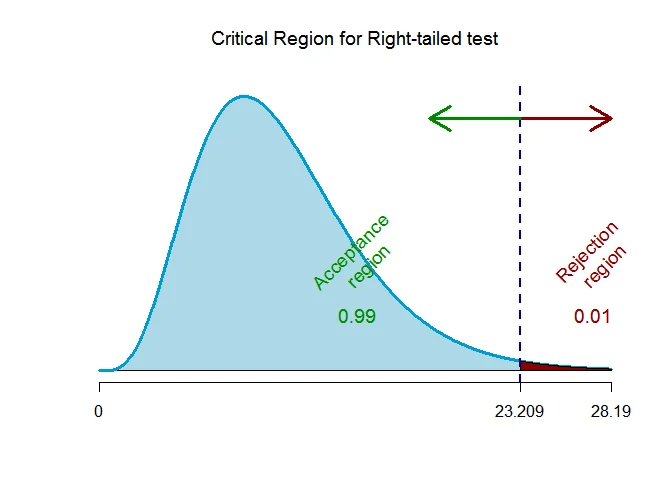
The rejection region (i.e. critical region) is $\chi^2 > 23.209$.
Step 5 Test Statistic
The test statistic under the null hypothesis is
$$ \begin{aligned} \chi^2& =\frac{(n-1)s^2}{\sigma^2_0}\\ &= \frac{(11-1)*(2.3)^2}{(2)^2}\\ &= 13.225 \end{aligned} $$
Step 6 Decision (Traditional approach)
The test statistic is $\chi^2 =13.225$ which falls $outside$ the critical region, we $\text{fail to reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value Approach)
This is a $\text{right-tailed}$ test, so the p-value is the area to the left of the test statistic ($\chi^2=13.225$) is p-value = $0.2114$.
The p-value is $0.2114$ which is $\text{greater than}$ the significance level of $\alpha = 0.01$, we $\text{fail to reject}$ the null hypothesis.
Example 3
A cigarette manufacturer wishes to test the claim that the variance of nicotine content of its cigarettes is 0.644. Nicotine content is measured in milligrams and is assumed normally distributed. A sample of 20 cigarettes has a standard deviation of 1.00 milligram. At $\alpha = 0.01$, is there enough evidence to reject the manufacturer’s claim?
Solution
Given that the sample size $n = 20$ and sample standard deviation $s = 1$.
Step 1 Hypothesis Problem
The hypothesis testing problem is $H_0 : \sigma^2 = 0.644$ against $H_1 : \sigma^2 \neq 0.644$ ($\text{two-tailed}$)
Step 2 Test Statistic
The test statistic for testing above hypothesis testing problem is
$$ \chi^2 =\frac{(n-1)s^2}{\sigma^2} $$
The test statistic follows chi-square distribution with $n-1$ degrees of freedom.
Step 3 Level of Significance
The significance level is $\alpha = 0.01$.
Step 4 Critical Value
As the alternative hypothesis is $\text{two-tailed}$, the critical values of $\chi^2$ for $\alpha=0.01$ level of significance and $n-1 = 19$ degrees of freedom $\text{ are }$ $\text{6.844 and 38.582}$ (from $\chi^2$ statistical table).
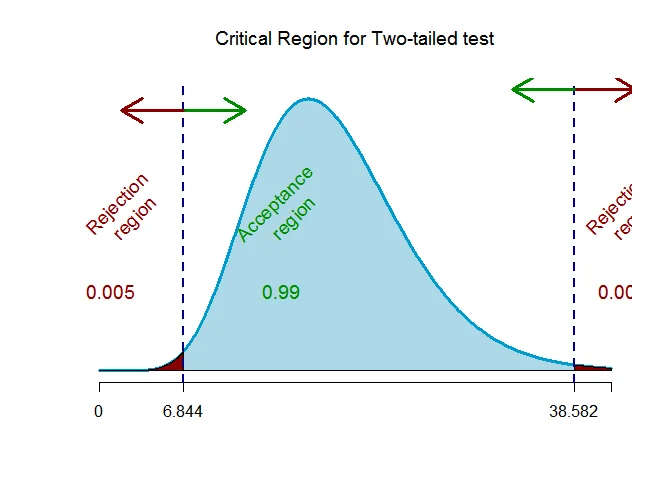
The rejection region (i.e. critical region) is $\chi^2 < 6.844$ or $\chi^2 > 38.582$.
Step 5 Test Statistic
The test statistic under the null hypothesis is
$$ \begin{aligned} \chi^2 &=\frac{(n-1)s^2}{\sigma^2_0}\\ &= \frac{(20-1)*(1)^2}{(0.8024961)^2}\\ &= 29.503 \end{aligned} $$
Step 6 Decision (Traditional approach)
The test statistic is $\chi^2 =29.503$ which falls $outside$ the critical region, we $\text{fail to reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value Approach)
This is a $\text{two-tailed}$ test, so the p-value is the area to the left of the test statistic ($\chi^2=29.503$) is p-value = $0.0585$.
The p-value is $0.0585$ which is $\text{greater than}$ the significance level of $\alpha = 0.01$, we $\text{fail to reject}$ the null hypothesis.
