Confidence Interval for the population mean when standard deviation is unknown
This tutorial covers examples on confidence interval for the population mean when the population standard deviation is unknown.
Example 1
A new brand of laptop battery is produced by a company. The company claims that the battery will last for an extended period of time before a recharge is necessary.
A sample of 40 batteries is tested for the length of usage time to recharge. The sample results are as follow:
Sample size: 40,
Sample Mean: 6.5 hrs,
Sample Standard Deviation: 1.3 hrs.
Construct a 99% confidence interval for the average length of usage time to recharge.
Solution
Given that sample size $n = 40$, sample mean $\overline{X}= 6.5$, sample standard deviation $s = 1.3$. The confidence level is $1-\alpha = 0.99$.
Step 1 Specify the confidence level $(1-\alpha)$
Confidence level is $1-\alpha = 0.99$. Thus, the level of significance is $\alpha = 0.01$.
Step 2 Given information
Given that sample size $n =40$, sample mean $\overline{X}=6.5$, sample standard deviation $s=1.3$.
Step 3 Specify the formula
$100(1-\alpha)$% confidence interval for the population mean $\mu$ is
$$ \begin{aligned} \overline{X} - E \leq \mu \leq \overline{X} + E \end{aligned} $$
where $E = t_{(\alpha/2,n-1)} \frac{s}{\sqrt{n}}$, and $t_{\alpha/2, n-1}$ is the $t$ value providing an area of $\alpha/2$ in the upper tail of the students’ $t$ distribution.
Step 4 Determine the critical value
The critical value of $t$ for given level of significance and $n-1$ degrees of freedom is $t_{\alpha/2,n-1}$.
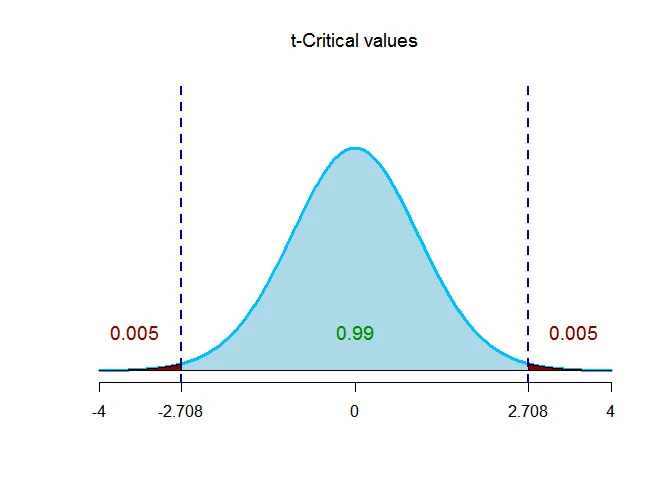
Thus $t_{\alpha/2,n-1} = t_{0.005,40-1}= 2.708$.
Step 5 Compute the margin of error
The margin of error for mean is
$$ \begin{aligned} E & = t_{(\alpha/2,n-1)} \frac{s}{\sqrt{n}}\\ & = 2.708 \frac{1.3}{\sqrt{40}} \\ & = 0.557. \end{aligned} $$
Step 6 Determine the confidence interval
$99$% confidence interval estimate for population mean is
$$ \begin{aligned} \overline{X} - E & \leq \mu \leq \overline{X} + E\\ 6.5 - 0.557 & \leq \mu \leq 6.5 + 0.557\\ 5.943 &\leq \mu \leq 7.057. \end{aligned} $$
Thus, $99$% confidence interval estimate for population mean is $(5.943,7.057)$.
Interpretation
We can be $99$% confident that the average length of usage time to recharge is between $5.943$ and $7.057$.
Example 2
Find the 95% confidence interval for the mean number of ounces of coffee that a machine dispenses in 12 ounce cups.
Assume the variable is normally distributed. The data is shown below:
12.03, 12.10, 12.02, 11.98, 12.00, 12.05, 11.97.
Solution
| $x_i$ | $x_i^2$ | |
|---|---|---|
| 12.03 | 144.72 | |
| 12.10 | 146.41 | |
| 12.02 | 144.48 | |
| 11.98 | 143.52 | |
| 12.00 | 144.00 | |
| 12.05 | 145.20 | |
| 11.97 | 143.28 | |
| Total | 84.15 | 1011.62 |
Sample mean
The sample mean of $X$ is
$$ \begin{aligned} \overline{x} &=\frac{1}{n}\sum_{i=1}^n x_i\\ &=\frac{84.15}{7}\\ &=12.0214\text{ ounce} \end{aligned} $$
The average of ounces of coffee is $12.0214$ ounce.
Sample variance
Sample variance of $X$ is
$$ \begin{aligned} s_x^2 &=\dfrac{1}{n-1}\bigg(\sum_{i=1}^{n}x_i^2-\frac{\big(\sum_{i=1}^n x_i\big)^2}{n}\bigg)\\ &=\dfrac{1}{6}\bigg(1011.6151-\frac{(84.15)^2}{7}\bigg)\\ &=\dfrac{1}{6}\big(1011.6151-\frac{7081.2225}{7}\big)\\ &=\dfrac{1}{6}\big(1011.6151-1011.60321\big)\\ &= \frac{0.01189}{6}\\ &=0.002 \end{aligned} $$
Sample standard deviation
The sample standard deviation is
$$ \begin{aligned} s_x &=\sqrt{s_x^2}\\ &=\sqrt{0.002}\\ &=0.0445 \text{ ounce} \end{aligned} $$
Sample size $n = 20$, sample mean $\overline{X}= 12.0214$, sample standard deviation $s = 0.0445$.
The confidence level is $1-\alpha = 0.95$.
Step 1 Specify the confidence level $(1-\alpha)$
Confidence level is $1-\alpha = 0.95$. Thus, the level of significance is $\alpha = 0.05$.
Step 2 Given information
Sample size $n =20$, sample mean $\overline{X}=12.0214$, sample standard deviation $s=0.0445$.
Step 3 Specify the formula
$100(1-\alpha)$% confidence interval for the population mean $\mu$ is
$$ \begin{aligned} \overline{X} - E \leq \mu \leq \overline{X} + E \end{aligned} $$
where $E = t_{(\alpha/2,n-1)} \frac{s}{\sqrt{n}}$, and $t_{\alpha/2, n-1}$ is the $t$ value providing an area of $\alpha/2$ in the upper tail of the students’ $t$ distribution.
Step 4 Determine the critical value
The critical value of $t$ for given level of significance and $n-1$ degrees of freedom is $t_{\alpha/2,n-1}$.
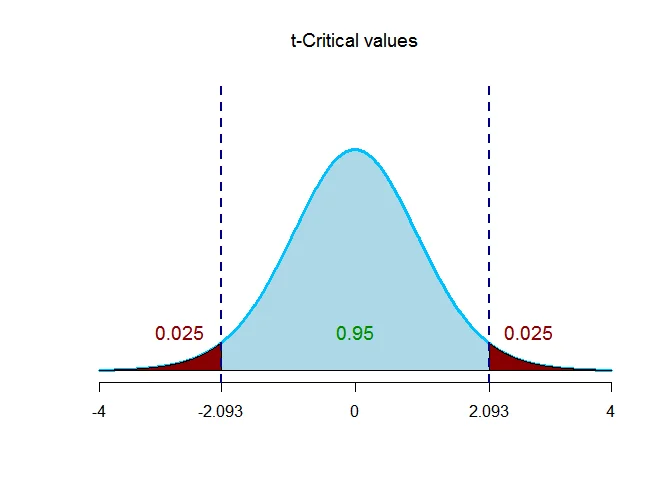
Thus $t_{\alpha/2,n-1} = t_{0.025,20-1}= 2.093$.
Step 5 Compute the margin of error
The margin of error for mean is
$$ \begin{aligned} E & = t_{(\alpha/2,n-1)} \frac{s}{\sqrt{n}}\\ & = 2.093 \frac{0.0445}{\sqrt{20}} \\ & = 0.0208. \end{aligned} $$
Step 6 Determine the confidence interval
$95$% confidence interval estimate for population mean is
$$ \begin{aligned} \overline{X} - E & \leq \mu \leq \overline{X} + E\\ 12.0214 - 0.021 & \leq \mu \leq 12.0214 + 0.021\\ 12.0006 &\leq \mu \leq 12.0422. \end{aligned} $$
Thus, $95$% confidence interval estimate for population mean is $(12.0006,12.0422)$.
Interpretation
We can be $95$% confident that the mean number of ounces of coffee that a machine dispenses in 12 ounce cups is between $12.0006$ and $12.0422$.