Confidence Interval for paired t-test
In this tutorial we will discuss how to determine confidence interval for the difference in means for dependent samples.
Example 1
An experiment ws designed to estimate the mean difference in weight gain for pigs fed ration A as compared with those fed ration B.
Eight pairs of pigs were used. The pigs within each pair were littermates. The rations were assigned at random to the two animals within each pair.
The gains (in pounds) after 45 days are shown below:
| Ration A | 65 | 37 | 40 | 47 | 49 | 65 | 53 | 59 |
|---|---|---|---|---|---|---|---|---|
| Ration B | 58 | 39 | 31 | 45 | 47 | 55 | 59 | 51 |
Assuming weight gain is normal, find the 95% confidence interval estimate for the mean of the differences $\mu_d$ where $d$= ration A - ration B.
Solution
| $x$ | $y$ | $d$ | $d-\overline{d}$ | $(d-\overline{d})^2$ | |
|---|---|---|---|---|---|
| 65 | 58 | 7 | 3.25 | 10.562 | |
| 37 | 39 | -2 | -5.75 | 33.062 | |
| 40 | 31 | 9 | 5.25 | 27.562 | |
| 47 | 45 | 2 | -1.75 | 3.062 | |
| 49 | 47 | 2 | -1.75 | 3.062 | |
| 65 | 55 | 10 | 6.25 | 39.062 | |
| 53 | 59 | -6 | -9.75 | 95.062 | |
| 59 | 51 | 8 | 4.25 | 18.062 | |
| Total | 30 | 229.5 |
The sample size $n= 8$.
The sample mean of the difference is
$$ \begin{aligned} \overline{d}&= \frac{1}{n}\sum_{i=1}^n d_i\\ &=\frac{30}{8}\\ &=3.75 \end{aligned} $$
and the sample standard deviation of the difference is
$$ \begin{aligned} s_d&= \sqrt{\frac{1}{n-1}\sum_{i=1}^n (d_i-\overline{d})^2}\\ &=\sqrt{\frac{229.5}{7}}\\ &=5.7259 \end{aligned} $$
The confidence level is $1-\alpha = 0.95$.
Step 1 Specify the confidence level
Confidence level = $1-\alpha = 0.95$, thus $\alpha = 0.05$.
Step 2 Given information
No. of matched pairs $n =8$. Sample mean of the difference is $\overline{d}=3.75$. Sample standard deviation of the difference is $s_d=5.726$.
Step 3 Specify the formula
$100(1-\alpha)$% confidence interval for the mean of the difference is
$$ \begin{equation*} \overline{d} - E \leq \mu_d \leq \overline{d} + E. \end{equation*} $$
where $E = t_{(\alpha/2,n-1)} \dfrac{s_d}{\sqrt{n}}$.
Step 4 Determine the critical value
The critical value $t$ with given level of significance and $n-1$ degrees of freedom is $t_{(\alpha/2,n-1)}$.
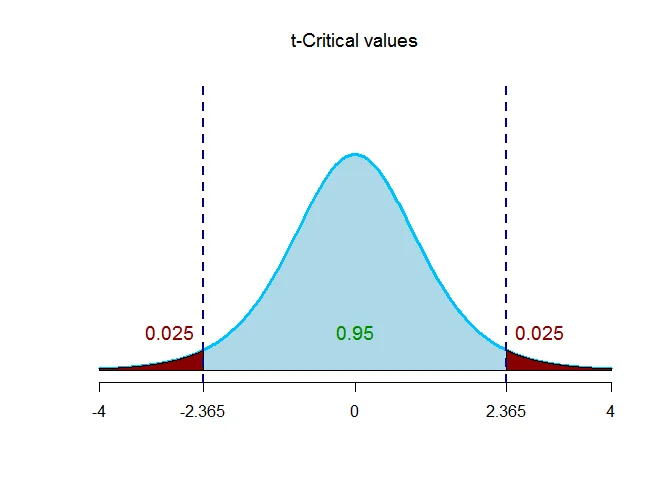
Thus $t_{(\alpha/2,n-1)}= t_{(0.025,8-1)} = 2.365$.
Step 5 Compute the margin of error
The margin of error is
$$ \begin{eqnarray*} E & = & t_{(\alpha/2,n-1)} \frac{s_d}{\sqrt{n}}\\ & = & 2.365 \frac{5.726}{\sqrt{8}}\\ & = & 4.788. \end{eqnarray*} $$
Step 6 Determine the confidence interval
$95$% confidence interval estimate for difference is
$$ \begin{eqnarray*} \overline{d} - E & & \leq \mu_d \leq \overline{d} + E\\ 3.75 - 4.788 & & \leq \mu_d \leq 3.75 + 4.788\\ -1.038 & &\leq \mu_d \leq 8.538. \end{eqnarray*} $$
Thus, $95$% confidence interval estimate for mean of the difference is $(-1.038,8.538)$.
Interpretation
We can be $95$% confident that the mean difference between before and after weight is between $-1.038$ and $8.538$.
Example 2
A one month weight loss program, for 7 people had the following results :
| Before weight | 150 | 130 | 160 | 155 | 146 | 144 | 141 |
|---|---|---|---|---|---|---|---|
| After weight | 152 | 127 | 159 | 157 | 142 | 143 | 139 |
Find a 98% confidence interval for the average difference between before and after weight.
Solution
| $x$ | $y$ | $d$ | $d-\overline{d}$ | $(d-\overline{d})^2$ | |
|---|---|---|---|---|---|
| 150 | 152 | -2 | -3 | 9 | |
| 130 | 127 | 3 | 2 | 4 | |
| 160 | 159 | 1 | 0 | 0 | |
| 155 | 157 | -2 | -3 | 9 | |
| 146 | 142 | 4 | 3 | 9 | |
| 144 | 143 | 1 | 0 | 0 | |
| 141 | 139 | 2 | 1 | 1 | |
| Total | 7 | 32 |
The sample size is $n = 7$.
The sample mean of the difference is
$$ \begin{aligned} \overline{d}&= \frac{1}{n}\sum_{i=1}^n d_i\\ &=\frac{7}{7}\\ &=1 \end{aligned} $$
and the sample standard deviation of the difference is
$$ \begin{aligned} s_d&= \sqrt{\frac{1}{n-1}\sum_{i=1}^n (d_i-\overline{d})^2}\\ &=\sqrt{\frac{32}{6}}\\ &=2.3094 \end{aligned} $$
The confidence level is $1-\alpha = 0.98$.
Step 1 Specify the confidence level
Confidence level = $1-\alpha = 0.98$, thus $\alpha = 0.02$.
Step 2 Given information
No. of matched pairs $n =7$. Sample mean of the difference is $\overline{d}=1$. Sample standard deviation of the difference is $s_d=2.309$.
Step 3 Specify the formula
$100(1-\alpha)$% confidence interval for the mean of the difference is
$$ \begin{equation*} \overline{d} - E \leq \mu_d \leq \overline{d} + E. \end{equation*} $$
where $E = t_{(\alpha/2,n-1)} \dfrac{s_d}{\sqrt{n}}$.
Step 4 Determine the critical value
The critical value $t$ with given level of significance and $n-1$ degrees of freedom is $t_{(\alpha/2,n-1)}$.
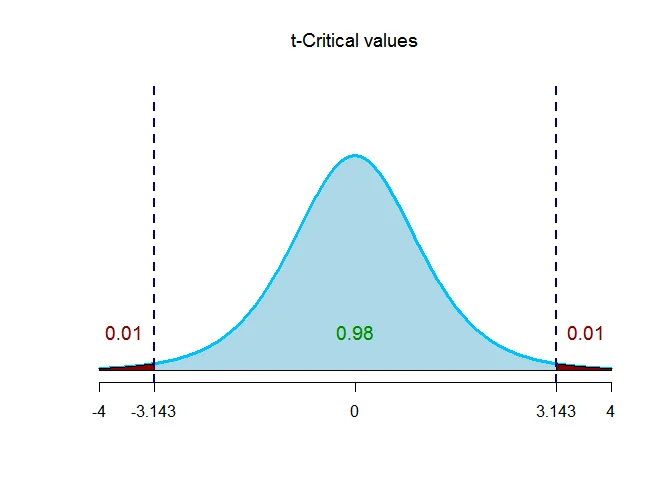
Thus $t_{(\alpha/2,n-1)}= t_{(0.01,7-1)} = 3.143$.
Step 5 Compute the margin of error
The margin of error is
$$ \begin{eqnarray*} E & = & t_{(\alpha/2,n-1)} \frac{s_d}{\sqrt{n}}\\ & = & 3.143 \frac{2.309}{\sqrt{7}}\\ & = & 2.743. \end{eqnarray*} $$
Step 6 Determine the confidence interval
$98$% confidence interval estimate for difference is
$$ \begin{eqnarray*} \overline{d} - E & & \leq \mu_d \leq \overline{d} + E\\ 1 - 2.743 & & \leq \mu_d \leq 1 + 2.743\\ -1.743 & &\leq \mu_d \leq 3.743. \end{eqnarray*} $$
Thus, $98$% confidence interval estimate for mean of the difference is $(-1.743,3.743)$.
Interpretation
We can be $98$% confident that the mean difference between before and after weight is between $-1.743$ and $3.743$.
Example 3
The owner of a small bakery has installed solar panels on the roof in the hope of reducing electricity costs.
For 8 months before the installation and 8 months immediately after, the monthly costs were as follows in hundreds of dollars:
| Before | 12 | 14 | 13 | 17 | 15 | 17 | 18 | 16 |
|---|---|---|---|---|---|---|---|---|
| After | 10 | 12 | 10 | 12 | 13 | 14 | 13 | 14 |
Find the 90% confidence interval estimate for the mean of reduction in electricity cost.
Solution
| $x$ | $y$ | $d$ | $d-\overline{d}$ | $(d-\overline{d})^2$ | |
|---|---|---|---|---|---|
| 12 | 10 | 2 | -1 | 1 | |
| 14 | 12 | 2 | -1 | 1 | |
| 13 | 10 | 3 | 0 | 0 | |
| 17 | 12 | 5 | 2 | 4 | |
| 15 | 13 | 2 | -1 | 1 | |
| 17 | 14 | 3 | 0 | 0 | |
| 18 | 13 | 5 | 2 | 4 | |
| 16 | 14 | 2 | -1 | 1 | |
| Total | 24 | 12 |
The sample size is $n = 8$.
The sample mean of the difference is
$$ \begin{aligned} \overline{d}&= \frac{1}{n}\sum_{i=1}^n d_i\\ &=\frac{24}{8}\\ &=3 \end{aligned} $$
and the sample standard deviation of the difference is
$$ \begin{aligned} s_d&= \sqrt{\frac{1}{n-1}\sum_{i=1}^n (d_i-\overline{d})^2}\\ &=\sqrt{\frac{12}{7}}\\ &=1.3093 \end{aligned} $$
The confidence level is $1-\alpha = 0.9$.
Step 1 Specify the confidence level
Confidence level = $1-\alpha = 0.9$, thus $\alpha = 0.1$.
Step 2 Given information
No. of matched pairs $n =8$. Sample mean of the difference is $\overline{d}=3$. Sample standard deviation of the difference is $s_d=1.309$.
Step 3 Specify the formula
$100(1-\alpha)$% confidence interval for the mean of the difference is
$$ \begin{equation*} \overline{d} - E \leq \mu_d \leq \overline{d} + E. \end{equation*} $$
where $E = t_{(\alpha/2,n-1)} \dfrac{s_d}{\sqrt{n}}$.
Step 4 Determine the critical value
The critical value $t$ with given level of significance and $n-1$ degrees of freedom is $t_{(\alpha/2,n-1)}$.
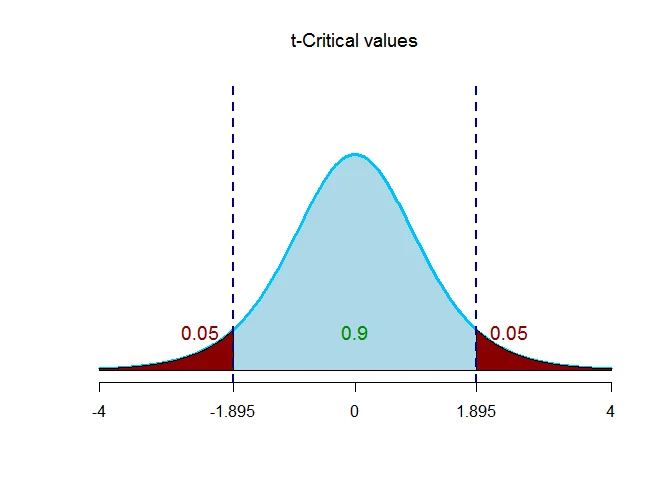
Thus $t_{(\alpha/2,n-1)}= t_{(0.05,8-1)} = 1.895$.
Step 5 Compute the margin of error
The margin of error is
$$ \begin{eqnarray*} E & = & t_{(\alpha/2,n-1)} \frac{s_d}{\sqrt{n}}\\ & = & 1.895 \frac{1.309}{\sqrt{8}}\\ & = & 0.877. \end{eqnarray*} $$
Step 6 Determine the confidence interval
$90$% confidence interval estimate for difference is
$$ \begin{eqnarray*} \overline{d} - E & & \leq \mu_d \leq \overline{d} + E\\ 3 - 0.877 & & \leq \mu_d \leq 3 + 0.877\\ 2.123 & &\leq \mu_d \leq 3.877. \end{eqnarray*} $$
Thus, $90$% confidence interval estimate for mean of the difference is $(2.123,3.877)$.
Interpretation
We can be $90$% confident that the mean reduction in electricity cost is between $2.123$ and $3.877$.
