Confidence Interval for Proportion
In this tutorial we will discuss some numerical examples to understand how to construct a confidence interval for population proportion.
Example 1
In a simple random sample of 50 animated children movies, 19 show tobacco use by main characters. Construct a 90% confidence interval to estimate the proportion of all animated children movies that show tobacco use by main characters. Assume the population is normally distributed.
Solution
Given that sample size $n = 50$, observed $X = 19$.
Thus the sample proportion of animated children movies that show tobacco use by main characters is
$\hat{p}=\frac{X}{n}=\frac{19}{50}=0.38$.
Step 1 Specify the confidence level $(1-\alpha)$
Confidence level is $1-\alpha = 0.9$. Thus, the level of significance is $\alpha = 0.1$.
Step 2 Given information
Given that sample size $n =50$, observed number of animated children movies that show tobacco use by main characters is $X=19$.
The estimate of the proportion of success is $\hat{p} =\frac{X}{n} =\frac{19}{50}=0.38$.
Step 3 Specify the formula
$100(1-\alpha)$% confidence interval for population proportion is
$$ \begin{aligned} \hat{p} - E \leq p \leq \hat{p} + E. \end{aligned} $$
where $E=Z_{\alpha/2} \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}$ and $Z_{\alpha/2}$ is the $Z$ value providing an area of $\alpha/2$ in the upper tail of the standard normal probability distribution.
Step 4 Determine the critical value
The critical value of $Z$ for given level of significance is $Z_{\alpha/2}$.
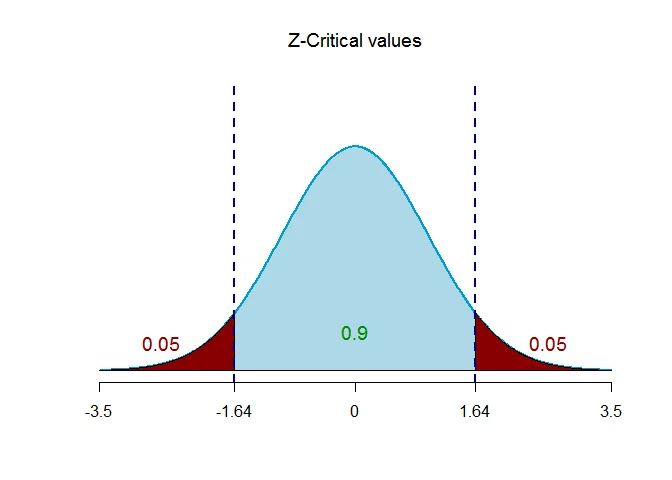
Thus $Z_{\alpha/2} = Z_{0.05} = 1.64$.
Step 5 Compute the margin of error
The margin of error for proportions is
$$ \begin{aligned} E & = Z_{\alpha/2} \sqrt{\frac{\hat{p}*(1-\hat{p})}{n}}\\ & = 1.64 \sqrt{\frac{0.38*(1-0.38)}{50}}\\ & =0.113. \end{aligned} $$
Step 6 Determine the confidence interval
$90$% confidence interval estimate for population proportion is
$$ \begin{aligned} \hat{p} - E & \leq p \leq \hat{p} + E\\ 0.38 - 0.113 & \leq p \leq 0.38 + 0.113\\ 0.2671 & \leq p \leq 0.4929. \end{aligned} $$
Thus, $90$% confidence interval estimate for population proportion $p$ is $(0.2671,0.4929)$.
Example 2
A marketing research firm wishes to estimate the proportion of adults who are planning to buy a new car in the next 6 months. A simple random sample of 100 adults led to 22 who were planning to buy a new car in the next 6 months.
Compute the 95% confidence interval for the proportion of adults who are planning to buy a new car in the next 6 months
Solution
Given that sample size $n = 100$, observed $X = 22$.
Thus the sample proportion adults who are planning to buy a new car in the next 6 months is
$\hat{p}=\frac{X}{n}=\frac{22}{100}=0.22$.
Step 1 Specify the confidence level $(1-\alpha)$
Confidence level is $1-\alpha = 0.95$. Thus, the level of significance is $\alpha = 0.05$.
Step 2 Given information
Given that sample size $n =100$, adults who are planning to buy a new car in the next 6 months is $X=22$.
The estimate of the proportion of adults who are planning to buy a new car in the next 6 months is $\hat{p} =\frac{X}{n} =\frac{22}{100}=0.22$.
Step 3 Specify the formula
$100(1-\alpha)$% confidence interval for population proportion is
$$ \begin{aligned} \hat{p} - E \leq p \leq \hat{p} + E. \end{aligned} $$
where $E=Z_{\alpha/2} \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}$ and $Z_{\alpha/2}$ is the $Z$ value providing an area of $\alpha/2$ in the upper tail of the standard normal probability distribution.
Step 4 Determine the critical value
The critical value of $Z$ for given level of significance is $Z_{\alpha/2}$.
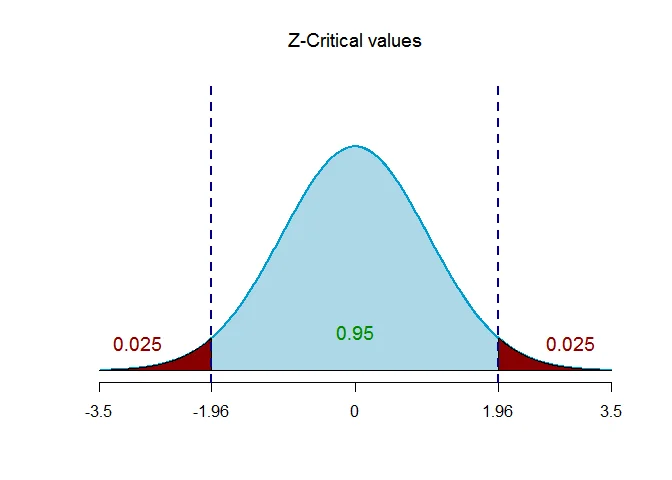
Thus $Z_{\alpha/2} = Z_{0.025} = 1.96$.
Step 5 Compute the margin of error
The margin of error for proportions is
$$ \begin{aligned} E & = Z_{\alpha/2} \sqrt{\frac{\hat{p}*(1-\hat{p})}{n}}\\ & = 1.96 \sqrt{\frac{0.22*(1-0.22)}{100}}\\ & =0.081. \end{aligned} $$
Step 6 Determine the confidence interval
$95$% confidence interval estimate for population proportion is
$$ \begin{aligned} \hat{p} - E & \leq p \leq \hat{p} + E\\ 0.22 - 0.081 & \leq p \leq 0.22 + 0.081\\ 0.1388 & \leq p \leq 0.3012. \end{aligned} $$
Thus, $95$% confidence interval estimate for population proportion $p$ is $(0.1388,0.3012)$.
