Laplace Distribution
A continuous random variable $X$ is said to have a Laplace
distribution (Double exponential distribution or bilateral
exponential distribution), if its p.d.f. is given by
$$ \begin{equation*} f(x;\mu, \lambda)=\left\{ \begin{array}{ll} \frac{1}{2\lambda}e^{-\frac{|x-\mu|}{\lambda}}, & \hbox{$-\infty < x< \infty$;} \\ & \hbox{$-\infty < \mu < \infty$, $\lambda >0$;} \\ 0, & \hbox{Otherwise.} \end{array} \right. \end{equation*} $$
In Laplace distribution $\mu$ is called location parameter, since it locates the curve of the distribution, and $\lambda$ is called scale parameter, since the shape of the curve depends on the value of $\lambda$.
Clearly, $f(x)\geq 0$ for all $x$ and
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \int_{-\infty}^\infty f(x; \mu, \lambda) \; dx &=& \int_{-\infty}^\mu f(x; \mu, \lambda) \; dx + \int_\mu^\infty f(x; \mu, \lambda)\; dx \\ &=& \int_{-\infty}^\mu \frac{1}{2\lambda}e^{-\frac{|x-\mu|}{\lambda}} \; dx + \int_\mu^\infty \frac{1}{2\lambda}e^{-\frac{|x-\mu|}{\lambda}}\; dx \\ \\ &=& \frac{1}{2\lambda}\bigg[\lambda e^{-\frac{|x-\mu|}{\lambda}}\bigg]_{-\infty}^\mu+ \frac{1}{2\lambda}\bigg[-\lambda e^{-\frac{|x-\mu|}{\lambda}}\bigg]_\mu^{-\infty}\\ &=& \frac{1}{2} + \frac{1}{2}=1. \end{eqnarray*} $$
Hence, $f(x)$ is a legitimate probability density function.
In notation, $X\sim L(\mu, \lambda)$.
Graph of Laplace Distribution
The graph of Laplace distribution with mean $\mu=0$ and for various values of $\lambda$ is as follows
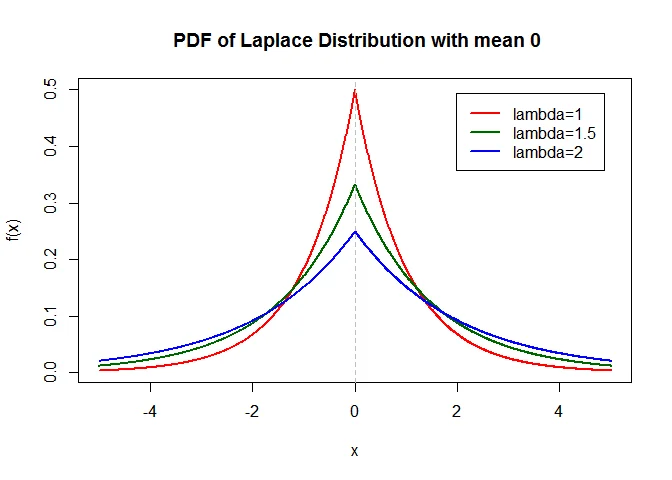
Standard Laplace Distribution
If we let $\mu=0$ and $\lambda =1$ in the Laplace distribution, then the distribution is known as Standard Laplace Distribution. The p.d.f of standard Laplace distribution is
$$ \begin{equation*} f(x)=\left\{ \begin{array}{ll} \frac{1}{2}e^{-|x|}, & \hbox{$-\infty < x< \infty$;} \\ & \\ 0, & \hbox{Otherwise.} \end{array} \right. \end{equation*} $$
Mean of Laplace Distribution
The mean of Laplace distribution is $E(X) = \mu$.
Proof
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \text{Mean = } E(X) &=& \int_{-\infty}^\infty xf(x)\; dx \\ &=& \int_{-\infty}^\infty (x-\mu+\mu)f(x)\; dx \\ &=& \int_{-\infty}^\infty (x-\mu)f(x)\; dx+\int_{-\infty}^\infty \mu f(x)\; dx \\ &=& I_1+\mu I_2, \end{eqnarray*} $$
In $I_1$, put $(x-\mu)=y$, therefore $dx=dy$,
$$ \begin{eqnarray*} \therefore I_1 & = & \frac{1}{2\lambda}\int_{-\infty}^\infty y e^{-\lambda|y|}\; dy = 0,\qquad \text{ ($\because$ integrand is an odd function)}\\ \text{ and } I_2 & = & \int_{-\infty}^\infty f(x) dx =1. \end{eqnarray*} $$
Therefore, $E(X) = 0 + \mu \cdot 1 = \mu$.
Thus, the mean of Laplace distribution is $\mu$.
Variance of Laplace Distribution
The variance of Laplace distribution is $V(X) = 2\lambda^2$.
Proof
The variance of random variable $X$ is given by
$$ \begin{equation*} V(X) = E(X^2) - [E(X)]^2. \end{equation*} $$
Let us find the expected value of $X^2$.
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) E(X^2) &=& \int_{-\infty}^\infty x^2f(x)\; dx \\ &=& \int_{-\infty}^\infty x^2\frac{1}{2\lambda} e^{-\frac{|x-\mu|}{\lambda}}\; dx. \end{eqnarray*} $$
Let $z=\frac{x-\mu}{\lambda}$, $\Rightarrow x =\mu+\lambda z$.
So, $dz = \frac{1}{\lambda} dx$. Hence,
`$$
\begin{eqnarray*}
% \nonumber to remove numbering (before each equation)
E(X^2) & = & \frac{1}{2}\int_{-\infty}^\infty (\mu
- \lambda z)^2 e^{-|z|}; dz.\ & = &\frac{1}{2} \int_{-\infty}^\infty \big(\mu^2 +2\mu \lambda z +\lambda^2 z^2\big) e^{-|z|}; dz.\ & = &\mu^2 \int_{-\infty}^\infty \frac{1}{2}e^{-|z|}; dz +\lambda \mu \int_{-\infty}^\infty z e^{-|z|}; dz+\frac{\lambda^2}{2}\int_{-\infty}^\infty z^2 e^{-|z|}; dz.\ & = & \mu^2 (1) + 0 + \frac{\lambda^2}{2}\int_{-\infty}^\infty z^2 e^{-|z|}; dz.\ &=& \mu^2 +\frac{2\lambda^2}{2}\int_0^\infty z^2 e^{-z};dz\ &=& \mu^2 +\lambda^2\frac{\Gamma 3}{1^3}\ &=& \mu^2 +2\lambda^2. \end{eqnarray*} $$` Thus, $V(X) =E[X^2]-[E(X)]^2 = \mu^2 -\mu^2+2\lambda^2 =2\lambda^2$.
Distribution Function of Laplace Distribution
The distribution function of Laplace distribution is
$$ \begin{equation*} F(x) = \left\{ \begin{array}{ll} \frac{1}{2}e^{\frac{(x-\mu)}{\lambda}}, & \hbox{$x< \mu$;} \\ &\\ 1-\frac{1}{2}e^{-\frac{(x-\mu)}{\lambda} }, & \hbox{$x\geq \mu$;} \end{array} \right. \end{equation*} $$
Proof
Distribution function of Laplace distribution is given by
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) F(x) &=& P(X\leq x) \\ &=& \int_{-\infty}^x f(t) \; dt\\ &=& \int_{-\infty}^x \frac{1}{2\lambda}e^{-\frac{(t-\mu)}{\lambda}} \; dt \end{eqnarray*} $$
Case I
When $x< \mu$, $\Rightarrow x-\mu < 0 \Rightarrow |x-\mu| =
-(x-\mu)$,
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \therefore F(x) &=& \int_{-\infty}^x \frac{1}{2\lambda} e^{\frac{(t-\mu)}{\lambda}}\; dt \\ &=& \frac{1}{2\lambda} \bigg[\lambda e^{\frac{(t-\mu)}{\lambda}}\bigg]_{-\infty}^x\\ &=& \frac{1}{2} e^{\frac{(x-\mu)}{\lambda}},\qquad x<\mu. \end{eqnarray*} $$
Case II
When $x\geq \mu$, $\Rightarrow x-\mu > 0 \Rightarrow |x-\mu| =
(x-\mu)$,
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \therefore F(x) &=& \int_{-\infty}^x \frac{1}{2 \lambda} e^{-\frac{(t-\mu)}{\lambda}}\; dt \\ &=& \frac{1}{2\lambda}\int_{-\infty}^\mu e^{\frac{(t-\mu)}{\lambda}}\; dt+ \frac{1}{2\lambda}\int_{\mu}^x \frac{\lambda}{2} e^{-\frac{(t-\mu)}{\lambda}}\; dt \\ &=& \frac{1}{2 \lambda} \bigg[\lambda e^{\frac{(t-\mu)}{\lambda}}\bigg]_{-\infty}^\mu+ \frac{1}{2\lambda} \bigg[-\lambda e^{-\frac{(t-\mu)}{\lambda}}\bigg]_{\mu}^x\\ &=& \frac{1}{2}[1-0]+\frac{1}{2} \big(-e^{-\frac{(x-\mu)}{\lambda}}+1\big)\\ & =& 1- \frac{1}{2}e^{-\frac{(x-\mu)}{\lambda}},\qquad x \geq \mu. \end{eqnarray*} $$
Therefore, the distribution function of Laplace distribution is
$$ \begin{equation*} F(x) = \left\{ \begin{array}{ll} \frac{1}{2}e^{\frac{(x-\mu)}{\lambda}}, & \hbox{$x< \mu$;} \\ &\\ 1-\frac{1}{2}e^{-\frac{(x-\mu)}{\lambda}}, & \hbox{$x\geq \mu$;} \end{array} \right. \end{equation*} $$
Quartiles of Laplace Distribution
The quartiles of Laplace distribution are $Q_1 = \mu + \dfrac{1}{\lambda}\log_e(0.5)$, $Q_2 = \mu$ and $Q_3 =\mu - \dfrac{1}{\lambda}\log_e(0.5)$.
Proof
The distribution function of Laplace distribution is
$$ \begin{equation*} F(x) = \left\{ \begin{array}{ll} \frac{1}{2}e^{\lambda(x-\mu)}, & \hbox{$x< \mu$;} \\ &\\ 1-\frac{1}{2}e^{-\lambda(x-\mu)}, & \hbox{$x\geq \mu$;} \end{array} \right. \end{equation*} $$
We have,
$$ \begin{equation*} F(Q_i) = P(X\leq Q_i) = \frac{i}{4},\quad i=1,2,3. \end{equation*} $$
For first quartile, $Q_1<\mu$,
$$ \begin{eqnarray*} F(Q_1) & = & \frac{1}{2}e^{\lambda(Q_1-\mu)}=\frac{1}{4}\\ \Rightarrow& & e^{\lambda(Q_1-\mu)}=\frac{1}{2} \\ \Rightarrow & &\lambda(Q_1-\mu)=\log_e(0.5)\\ \Rightarrow & & Q_1 = \mu + \frac{1}{\lambda}\log_e(0.5). \end{eqnarray*} $$
For second quartile, $Q_2\geq\mu$,
$$ \begin{eqnarray*} F(Q_2) & = & 1-\frac{1}{2}e^{-\lambda(Q_2-\mu)}=\frac{1}{2}\\ \Rightarrow& & e^{-\lambda(Q_2-\mu)}=1\\ \Rightarrow & & -\lambda(Q_2-\mu)=0\\ \Rightarrow & & Q_2 = \mu. \end{eqnarray*} $$
For third quartile, $Q_3\geq\mu$,
$$ \begin{eqnarray*} F(Q_3) & = & 1-\frac{1}{2}e^{-\lambda(Q_3-\mu)}=\frac{3}{4}\\ \Rightarrow& & \frac{1}{2}e^{-\lambda(Q_3-\mu)}=\frac{1}{4}\\ \Rightarrow & &-\lambda(Q_3-\mu)=\log_e(0.5)\\ \Rightarrow & & Q_3 = \mu-\frac{1}{\lambda}\log_e(0.5). \end{eqnarray*} $$
M.G.F. of Laplace Distribution
The moment generating function of Laplace distribution is
$$ \begin{equation*} M_X(t) = e^{t\mu}\bigg(1-\frac{t^2}{\lambda^2}\bigg)^{-1}. \end{equation*} $$
Proof
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) M_X(t) &=& E(e^{tX}) \\ &=& \int_{-\infty}^\infty e^{tx}f(x) \; dx\\ &=& \int_{-\infty}^\infty e^{t(x-\mu+\mu)}f(x) \; dx\\ &=& \frac{\lambda}{2}e^{t\mu}\int_{-\infty}^\infty e^{t(x-\mu)}e^{-\lambda|x-\mu|} \; dx \end{eqnarray*} $$
Let $(x-\mu) =y$, therefore $dx=dy$.
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) M_X(t) &=& \frac{\lambda}{2}e^{t\mu}\int_{-\infty}^\infty e^{ty}e^{-\lambda|y|} \; dy\\ &=& \frac{\lambda}{2}e^{t\mu}\bigg[\int_{-\infty}^0 e^{ty}e^{\lambda y} \;dy +\int_0^{\infty} e^{ty}e^{-\lambda y}\; dy\bigg]\\ &=& \frac{\lambda}{2}e^{t\mu}\bigg[\int_{-\infty}^0 e^{(t+\lambda)y}\;dy +\int_0^{\infty} e^{-(\lambda -t)y}\; dy \bigg]\\ &=& \frac{\lambda}{2}e^{t\mu}\bigg\{\bigg[\frac{e^{(t+\lambda)y}}{t+\lambda}\bigg]_{-\infty}^0+\bigg[\frac{e^{-(\lambda-t)y}}{-(\lambda-t)}\bigg]_0^{\infty}\bigg\}\\ &=& \frac{\lambda}{2}e^{t\mu}\bigg\{\bigg[\frac{1}{t+\lambda}-0\bigg]+\bigg[0-\frac{1}{t-\lambda}\bigg]\bigg\}\\ &=& \frac{\lambda}{2}e^{t\mu}\bigg(\frac{-2\lambda}{t^2-\lambda^2}\bigg)\\ &=& e^{t\mu}\bigg(\frac{\lambda^2}{\lambda^2-t^2}\bigg)\\ &=& e^{t\mu}\bigg(1-\frac{t^2}{\lambda^2}\bigg)^{-1}\\ &=& e^{t\mu}\sum_{r=0}^\infty \bigg(\frac{t^2}{\lambda^2}\bigg)^r. \end{eqnarray*} $$
C.G.F. of Laplace Distribution
The cumulant generating function of Laplace distribution $L(\mu,\lambda)$ is
$K_X(t)=\mu t - \log_e \bigg(1-\frac{t^2}{r^2}\bigg)$.
Proof
By definition of c.g.f.,
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) K_X(t) &=& \log_e M_X(t) \\ &=& \log_e \bigg[e^{t\mu} \bigg(1-\frac{t^2}{r^2}\bigg)^{-1} \bigg]\\ &=& \mu t - \log_e \bigg(1-\frac{t^2}{r^2}\bigg)\\ &=& \mu t +\bigg(\frac{t^2}{\lambda^2} + \frac{t^4}{2\lambda^4}+\cdots\bigg)\\ & & \qquad (\because \log (1-x) = -(x+\frac{x^2}{2}+\frac{x^3}{3}+\cdots). \end{eqnarray*} $$
Cumulants
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \kappa_1 =\mu_1^\prime &=& \text{coefficient of $t$ in the expansion of $K_X(t)$}= \mu. \end{eqnarray*} $$
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \kappa_2 =\mu_2 &=& \text{coefficient of $\frac{t^2}{2!}$ in the expansion of $K_X(t)$} \\ &=& \frac{2}{\lambda^2}=\text{ variance }. \end{eqnarray*} $$
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \kappa_3 =\mu_3 &=& \text{coefficient of $\frac{t^3}{3!}$ in the expansion of $K_X(t)$} \\ &=& 0 \end{eqnarray*} $$
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \kappa_4 =\mu_4-3\mu_2^2&=& \text{coefficient of $\frac{t^4}{4!}$ in the expansion of $K_X(t)$} \\ &=& \frac{12}{\lambda^4}. \end{eqnarray*} $$
Hence
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \mu_4 & = & \kappa_4 + 3\kappa_2^2 =\frac{12}{\lambda^4}+\frac{12}{\lambda^4}=\frac{24}{\lambda^4}. \end{eqnarray*} $$
In general, the $r^{th}$ cumulant is given by
$$ \begin{equation*} \kappa_r= \left\{ \begin{array}{ll} 0, & \hbox{if $r$ is odd except 1;} \\ &\\ \dfrac{2(r-1)!}{\lambda^r}, & \hbox{if $r$ is even} \end{array} \right. \end{equation*} $$
Characteristics Function
The characteristic function of Laplace distribution is
$$ \begin{equation*} \phi_X(t) = e^{it\mu}\bigg(1+\frac{t^2}{\lambda^2}\bigg)^{-1}. \end{equation*} $$
Proof
Let $X\sim L(\mu,\lambda)$ distribution. Then the M.G.F. of Laplace distribution is
$$ \begin{equation*} M_X(t) = e^{t\mu} \bigg(1- \frac{t^2}{\lambda^2}\bigg)^{-1}. \end{equation*} $$
The characteristics function of $X$ is
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \phi_{X}(t) &=& E(e^{itX}) \\ &=& M_X(it)\\ &=& e^{it\mu} \bigg(1- \frac{(it)^2}{\lambda^2}\bigg)^{-1}\\ &=& e^{it\mu} \bigg(1- \frac{i^2t^2}{\lambda^2}\bigg)^{-1}\\ &=& e^{it\mu} \bigg(1+ \frac{t^2}{\lambda^2}\bigg)^{-1}. \end{eqnarray*} $$
If $X\sim L(0,1)$, then the characteristics function of Standard Laplace distribution is
$$ \begin{equation*} \phi_X(t)=(1+t^2)^{-1} =\frac{1}{1+t^2}. \end{equation*} $$
$r^{th}$ moment of Laplace Distribution
The $r^{th}$ moment of Laplace distribution is
$$ \begin{equation*} \mu_r^\prime =\frac{1}{2} \sum_{k=0}^r\binom{r}{k} \mu^{r-k} \frac{k!}{\lambda^k} ((-1)^k +1). \end{equation*} $$
Proof
Let $X\sim L(\mu,\lambda)$. Then the pdf of $X$ is
$$ \begin{equation*} f(x) =\frac{\lambda}{2}e^{-\lambda |x-\mu|}, -\infty <x<\infty, -\infty< \mu<\infty, \lambda>0. \end{equation*} $$
The $r^{th}$ moment of Laplace distribution is
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \mu_r^\prime &=& E(X^r) \\ &=& \frac{\lambda}{2}\int_{-\infty}^\infty x^r e^{-\lambda|x-\mu|} \end{eqnarray*} $$
Let $Z =\lambda (X-\mu)$, $x = \mu +\frac{z}{\lambda}$. Thus $dx = \frac{1}{\lambda} dz$.
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \mu_r^\prime &=& \frac{\lambda}{2} \int_{-\infty}^\infty (\mu+\frac{z}{\lambda})^r e^{-|z|} \frac{1}{\lambda}\; dz\\ &=& \frac{1}{2}\int_{-\infty}^\infty \sum_{k=0}^r\binom{r}{k} \bigg(\frac{z}{\lambda}\bigg)^k \mu^{r-k} e^{-|z|}\; dz\\ &=& \frac{1}{2} \sum_{k=0}^r\binom{r}{k} \mu^{r-k} \frac{1}{\lambda^k} \int_{-\infty}^\infty z^k e^{-|z|}\;dz\\ &=& \frac{1}{2} \sum_{k=0}^r\binom{r}{k} \mu^{r-k} \frac{1}{\lambda^k} \bigg[(-1)^k \int_{0}^\infty z^k e^{-z}\;dz+\int_{0}^\infty z^k e^{-z}\;dz\bigg]\\ &=&\frac{1}{2} \sum_{k=0}^r\binom{r}{k} \mu^{r-k} \frac{1}{\lambda^k} \bigg[(-1)^k \Gamma(k+1) +\Gamma (k+1)\bigg]\\ &=&\frac{1}{2} \sum_{k=0}^r\binom{r}{k} \mu^{r-k} \frac{k!}{\lambda^k} ((-1)^k +1). \end{eqnarray*} $$
Result
Let $X$ and $Y$ be two i.i.d. exponential variate with parameter $\theta$. The distribution of $(X-Y)$ is Laplace distribution.
(i.e., The difference of two independent exponential variate is Laplace variate.)
Solution
$X$ and $Y$ be two i.i.d. exponential variate with parameter
$\theta$. Then p.d.f. of $x$ is
$$ \begin{equation*} f_X(x) = \theta e^{-\theta x}; \quad x> 0, \theta>0 \end{equation*} $$
and p.d.f. of $Y$ is
$$ \begin{equation*} f_Y(y) = \theta e^{-\theta y}; \quad y> 0, \theta>0 \end{equation*} $$
The m.g. f. of $X$ is $M_X(t) =\bigg(1-\dfrac{t}{\theta}\bigg)^{-1}$. Let $U=X-Y$. Then the m.g.f. of $U$ is
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) M_U(t) = E(e^{tU}) &=& E(e^{t(X_Y)}\\ &=& E(e^{tX})\cdot E(e^{-tY})\\ & = & M_X(t)\cdot M_Y(-t)\\ & = & \bigg(1-\frac{t}{\theta}\bigg)^{-1}\cdot \bigg(1+\frac{t}{\theta}\bigg)^{-1}\\ &=&\bigg(1-\frac{t^2}{\theta^2}\bigg)^{-1}. \end{eqnarray*} $$
which is the m.g.f. of Laplace distribution with $\mu= 0$ and $\lambda = \theta$. Hence, by uniqueness property of M.G.F., $U=X-Y\sim L(0,\theta)$ distribution.
