Plus Four Confidence Interval for Proportion

In this article we will discuss step by step examples to construct a plus four confidence interval for population proportion.

Example 1 Using Plus Four Confidence Interval for Proportion

In a random sample of 60 students from a college, 32 opted mathematics as major subject. Using plus four method find a 95% confidence interval for the proportion of students who opted mathematics as a major subject.

Solution

Given that sample size $n = 60$, observed $X = 32$.

The estimate of sample proportion of students who opted mathematics as a major subject based on plus four method is $\hat{p}=\dfrac{X+2}{n+4}=\dfrac{32+2}{60+4}=0.5312$.

Step 1 Specify the confidence level $(1-\alpha)$

Confidence level is $1-\alpha = 0.95$. Thus, the level of significance is $\alpha = 0.05$.

Step 2 Given information

Given that sample size $n =60$, observed number of students who opted mathematics as a major subject is $X=32$.

The estimate of the proportion of students who opted mathematics as a major subject based on plus four rule is $\hat{p} =\dfrac{X+2}{n+4} =\dfrac{32+2}{60+4}=0.5312$.

Step 3 Specify the plus four confidence interval formula

$100(1-\alpha)$% plus four confidence interval for population proportion is $$ \begin{aligned} \hat{p} - E \leq p \leq \hat{p} + E. \end{aligned} $$ where $E=Z_{\alpha/2} \sqrt{\dfrac{\hat{p}(1-\hat{p})}{n+4}}$ and $Z_{\alpha/2}$ is the $Z$ value providing an area of $\alpha/2$ in the upper tail of the standard normal probability distribution.

Step 4 Determine the critical value

The critical value of $Z$ for given level of significance is $Z_{\alpha/2}$.

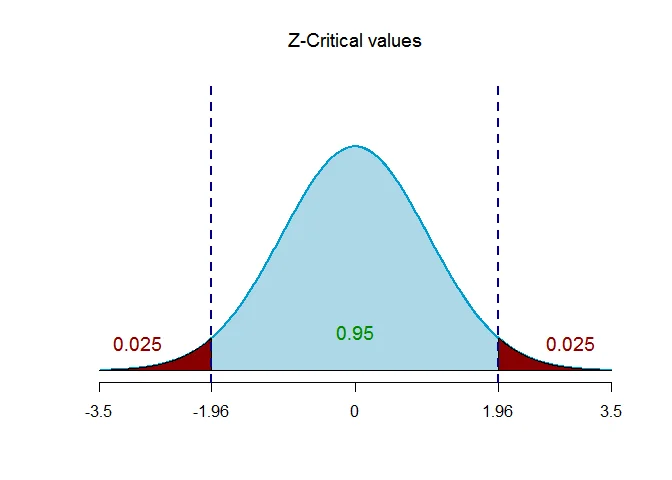
Thus $Z_{\alpha/2} = Z_{0.025} = 1.96$.

Step 5 Compute the margin of error

The margin of error for proportions is $$ \begin{aligned} E & = Z_{\alpha/2} \sqrt{\frac{\hat{p}*(1-\hat{p})}{n+4}}\\ & = 1.96 \sqrt{\frac{0.5312*(1-0.5312)}{60+4}}\\ & =0.1223. \end{aligned} $$

Step 6 Determine the plus four method confidence interval

$95$% plus four confidence interval estimate for population proportion is $$ \begin{aligned} \hat{p} - E & \leq p \leq \hat{p} + E\\ 0.5312 - 0.1223 & \leq p \leq 0.5312 + 0.1223\\ 0.4089 & \leq p \leq 0.6535. \end{aligned} $$ Thus, $95$% plus four confidence interval estimate for population proportion $p$ of students who opted mathematics as a major subject is $(0.4089,0.6535)$.

Example 2 Using Plus 4 Confidence Interval

A random sample of 20 college students was asked: “Have you smoked a cigarette in the past week?” eight students reported smoking within the past week. Use the plus four method to find a 98% confidence interval for the true proportion of college students who smoke.

Solution

Given that sample size $n = 20$, observed $X = 8$.

The estimate of sample proportion of students who smoked a cigarette in the past week based on plus four rule is $\hat{p}=\dfrac{X+2}{n+4}=\dfrac{8+2}{20+4}=0.4167$.

Step 1 Specify the confidence level $(1-\alpha)$

Confidence level is $1-\alpha = 0.98$. Thus, the level of significance is $\alpha = 0.02$.

Step 2 Given information

Given that sample size $n =20$, observed number of students who smoked a cigarette in the past week is $X=8$.

The estimate of the proportion of students who smoked a cigarette in the past week based on plus four rule is $\hat{p} =\dfrac{X+2}{n+4} =\dfrac{8+2}{20+4}=0.4167$.

Step 3 Specify the plus four confidence interval formula

$100(1-\alpha)$% plus four confidence interval for population proportion is $$ \begin{aligned} \hat{p} - E \leq p \leq \hat{p} + E. \end{aligned} $$ where $E=Z_{\alpha/2} \sqrt{\dfrac{\hat{p}(1-\hat{p})}{n+4}}$ and $Z_{\alpha/2}$ is the $Z$ value providing an area of $\alpha/2$ in the upper tail of the standard normal probability distribution.

Step 4 Determine the critical value

The critical value of $Z$ for given level of significance is $Z_{\alpha/2}$.

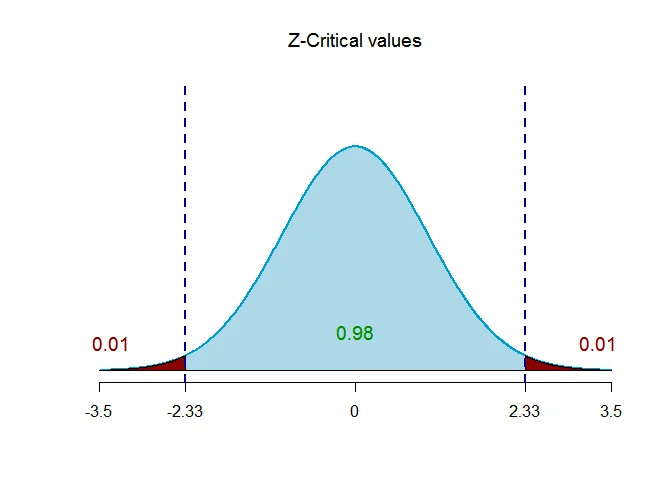
Thus $Z_{\alpha/2} = Z_{0.01} = 2.33$.

Step 5 Compute the margin of error

The margin of error for proportions is $$ \begin{aligned} E & = Z_{\alpha/2} \sqrt{\frac{\hat{p}*(1-\hat{p})}{n+4}}\\ & = 2.33 \sqrt{\frac{0.4167*(1-0.4167)}{20+4}}\\ & =0.2345. \end{aligned} $$

Step 6 Determine the plus four confidence interval

$98$% plus four method confidence interval estimate for population proportion is $$ \begin{aligned} \hat{p} - E & \leq p \leq \hat{p} + E\\ 0.4167 - 0.2345 & \leq p \leq 0.4167 + 0.2345\\ 0.1822 & \leq p \leq 0.6512. \end{aligned} $$ Thus, $98$% plus four confidence interval estimate for population proportion $p$ of students who smoked a cigarette in the past week is $(0.1822,0.6512)$.

Conclusion

Hope you like Plus four confidence interval for proportion tutorial and step by step explaination with examples. use calculator given in below link to calculate plus four confidence interval for propertion.

Read more about other Statistics Calculator on below links

Related Resources

Theory
Calculator