Two sample t test for means with unknown but equal variances
In this tutorial we will discuss some numerical examples on two sample t test for difference between two population means when the population variances are unknown but equal.
Example 1
A high school language course is given in two sections, each using a different teaching method. The first section has $21$ students, and the grades in that section have a mean of $82.6$ and a standard deviation of $8.6$. In the second section, with $43$ students, the mean of the grades is $85.2$, with a standard deviation of $7.9$. At $\alpha = 0.05$, test the hypothesis that the method used in second section is more effective. (Assume equal variances)
Solution
Given that the sample size $n_1 = 21$, $n_2 = 43$, sample mean $\overline{x}_1= 82.6$, $\overline{x}_2= 85.2$, sample standard deviation $s_1 = 8.6$ and $s_2 = 7.9$.
Step 1 State the hypothesis testing problem
The hypothesis testing problem is
$H_0 : \mu_1 = \mu_2$ (i.e., Methods used in both the sections are equally effective) against $H_1 : \mu_1 < \mu_2$ ($\textit{left-tailed}$) (i.e., Method used in second section is more effective that the method used in first section).
Step 2 Define test statistic
The test statistic is
$$ \begin{aligned} t& =\frac{(\overline{x}_1 -\overline{x}_1)-(\mu_1 - \mu_2)}{sp\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \end{aligned} $$
where the pooled standard deviation is
$$ \begin{aligned} s_p & = \sqrt{\frac{(n_1-1)s_1^2 +(n_2-1)s_2^2}{n_1+n_2-2}}\\ & = \sqrt{\frac{(21-1)8.6^2 +(43-1)7.9^2}{21+43-2}}\\ & = 8.1324. \end{aligned} $$
Step 3 Specify the level of significance
The significance level is $\alpha = 0.05$.
Step 4 Determine the critical value
As the alternative hypothesis is $\textit{left-tailed}$, the critical value of $t$ using $\alpha = 0.05$ and degrees of freedom $n_1+n_2-2=21+43-2=62$ $\text{is}$ $\text{-1.67}$.
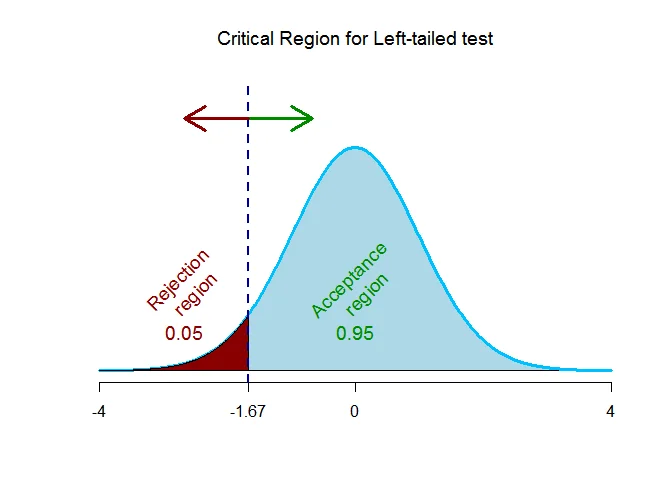
The rejection region (i.e. critical region) is $\text{t < -1.67}$.
Step 5 Computation
The test statistic under the null hypothesis is
$$ \begin{aligned} t&=\frac{(\overline{x}_1 -\overline{x}_1)-(\mu_1-\mu_2)}{sp\sqrt{\big(\frac{1}{n_1}+\frac{1}{n_2}\big)}}\\ &= \frac{(82.6-85.2)-0}{8.1324\sqrt{\big(\frac{1}{21}+\frac{1}{43}\big)}}\\ &= -1.2009 \end{aligned} $$
Step 6 Decision (Traditional approach)
The rejection region (i.e. critical region) is $\text{t < -1.67}$.
The test statistic is $t =-1.2009$ which falls $\text{outside}$ the critical region, we $\textit{fail to reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value approach)
The test is $\textit{left-tailed}$ test, so p-value is the area to the $\textit{left}$ of the test statistic ($t=-1.2009$). That is p-value = $P(t\leq -1.2009 ) = 0.1172$.
The p-value is $0.1172$ which is $\textit{greater than}$ the significance level of $\alpha = 0.05$, we $\textit{fail to reject}$ the null hypothesis.
Example 2
Eight culture of bacterium are split in half. Of half is tested using a standard antibiotic and the other half is tested using a new antibiotic. The time taken to kill the bacterium are given in the following table. Use an appropriate hypothesis test to assess our belief that the new antibiotic is quicker than the standard antibiotic. Use $\alpha = 0.01$.
| Bacterium Culture | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Standard Antibiotic | 23.6 | 27.9 | 22.9 | 21.8 | 25.8 | 30.7 | 26.5 | 25.4 |
| New Antibiotic | 22.5 | 25.6 | 24.0 | 20.4 | 26.0 | 26.6 | 26.4 | 22.1 |
Solution
Given that the sample size $n_1 = 8$, $n_2 = 8$, sample mean $\overline{x}_1= 25.575$, $\overline{x}_2= 24.2$, sample standard deviation $s_1 = 2.876$ and $s_2 = 2.317$.
Step 1 State the hypothesis testing problem
The hypothesis testing problem is
$H_0 : \mu_1 = \mu_2$ against $H_1 : \mu_1 > \mu_2$ ($\textit{right-tailed}$)
Step 2 Define test statistic
The test statistic is
$$ \begin{aligned} t& =\frac{(\overline{x}_1 -\overline{x}_1)-(\mu_1 - \mu_2)}{sp\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \end{aligned} $$
where the pooled standard deviation is
$$ \begin{aligned} s_p & = \sqrt{\frac{(n_1-1)s_1^2 +(n_2-1)s_2^2}{n_1+n_2-2}}\\ & = \sqrt{\frac{(8-1)2.8764^2 +(8-1)2.317^2}{8+8-2}}\\ & = 2.6117. \end{aligned} $$
Step 3 Specify the level of significance
The significance level is $\alpha = 0.01$.
Step 4 Determine the critical value
As the alternative hypothesis is $\textit{right-tailed}$, the critical value of $t$ using $\alpha = 0.01$ and degrees of freedom $n_1+n_2-2=8+8-2=14$ $\text{is}$ $\text{2.624}$.
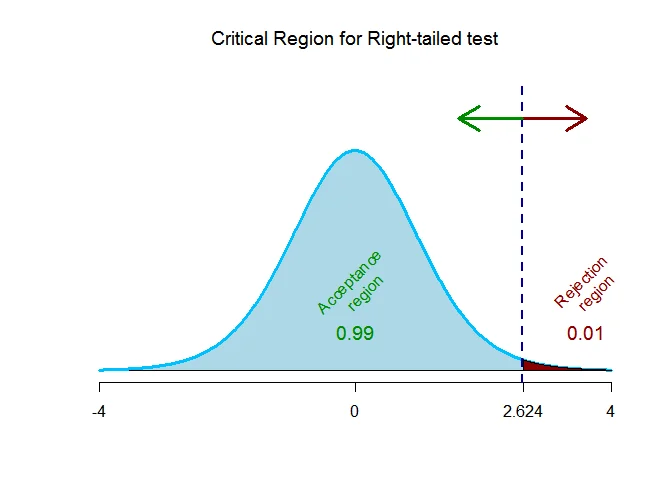
The rejection region (i.e. critical region) is $\text{t > 2.624}$.
Step 5 Computation
The test statistic under the null hypothesis is
$$ \begin{aligned} t&=\frac{(\overline{x}_1 -\overline{x}_1)-(\mu_1-\mu_2)}{sp\sqrt{\big(\frac{1}{n_1}+\frac{1}{n_2}\big)}}\\ &= \frac{(25.575-24.2)-0}{2.6117\sqrt{\big(\frac{1}{8}+\frac{1}{8}\big)}}\\ &= 1.053 \end{aligned} $$
Step 6 Decision (Traditional approach)
The rejection region (i.e. critical region) is $\text{t > 2.624}$.
The test statistic is $t =1.053$ which falls $\text{outside}$ the critical region, we $\textit{fail to reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value approach)
The test is $\textit{right-tailed}$ test, so p-value is the area to the $\textit{right}$ of the test statistic ($t=1.053$). That is p-value = $P(t\geq 1.053 ) = 0.1551$.
The p-value is $0.1551$ which is $\textit{greater than}$ the significance level of $\alpha = 0.01$, we $\textit{fail to reject}$ the null hypothesis.
Example 3
A rope company produces ropes on two production lines. The tensile strength is an important measure of quality. A test of randomly selected ropes yields the following results:
| Summary | Rope 1 | Rope 2 |
|---|---|---|
| Mean Tensile Strength | 7087 kg | 7200 kg |
| SD | 425kg | 415kg |
| Sample size | 25 | 20 |
The company assumes the populations of rope tensile strengths are approximately normal with equal variances. The company suspects there is a difference in the mean values of the populations. Conduct an appropriate hypothesis test at the 0.05 significance level.
Solution
Given that the sample size $n_1 = 25$, $n_2 = 20$, sample mean $\overline{x}_1= 7087$, $\overline{x}_2= 7200$, sample standard deviation $s_1 = 425$ and $s_2 = 415$.
Step 1 State the hypothesis testing problem
The hypothesis testing problem is
$H_0 : \mu_1 = \mu_2$ against $H_1 : \mu_1 \neq \mu_2$ ($\textit{two-tailed}$)
Step 2 Define test statistic
The test statistic is
$$ \begin{aligned} t& =\frac{(\overline{x}_1 -\overline{x}_1)-(\mu_1 - \mu_2)}{sp\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \end{aligned} $$
where the pooled standard deviation is
$$ \begin{aligned} s_p & = \sqrt{\frac{(n_1-1)s_1^2 +(n_2-1)s_2^2}{n_1+n_2-2}}\\ & = \sqrt{\frac{(25-1)425^2 +(20-1)415^2}{25+20-2}}\\ & = 420.6107. \end{aligned} $$
Step 3 Specify the level of significance
The significance level is $\alpha = 0.05$.
Step 4 Determine the critical value
As the alternative hypothesis is $\textit{two-tailed}$, the critical value of $t$ using $\alpha = 0.05$ and degrees of freedom $n_1+n_2-2=25+20-2=43$ $\text{are}$ $\text{-2.017 and 2.017}$.
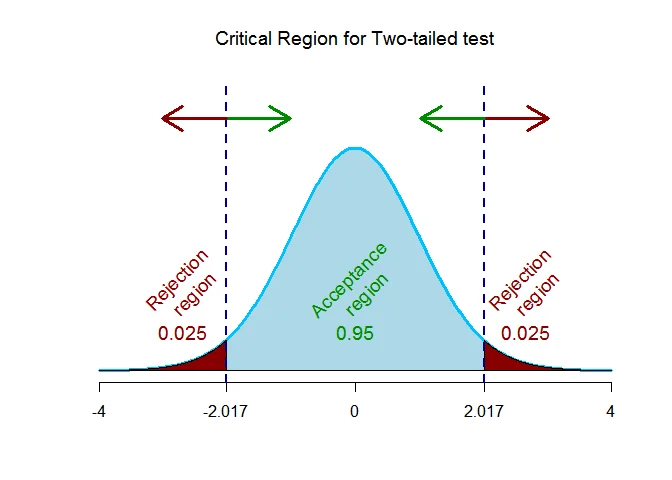
The rejection region (i.e. critical region) is $\text{t < -2.017 or t > 2.017}$.
Step 5 Computation
The test statistic under the null hypothesis is
$$ \begin{aligned} t&=\frac{(\overline{x}_1 -\overline{x}_1)-(\mu_1-\mu_2)}{sp\sqrt{\big(\frac{1}{n_1}+\frac{1}{n_2}\big)}}\\ &= \frac{(7087-7200)-0}{420.6107\sqrt{\big(\frac{1}{25}+\frac{1}{20}\big)}}\\ &= -0.8955 \end{aligned} $$
Step 6 Decision (Traditional approach)
The rejection region (i.e. critical region) is $\text{t < -2.017 or t > 2.017}$.
The test statistic is $t =-0.8955$ which falls $\text{outside}$ the critical region, we $\textit{fail to reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value approach)
The test is $\textit{two-tailed}$ test, so p-value is the area to the $\textit{extreme}$ of the test statistic ($t=-0.8955$). That is p-value = $2*P(t\geq 0.8955 ) = 0.3755$.
The p-value is $0.3755$ which is $\textit{greater than}$ the significance level of $\alpha = 0.05$, we $\textit{fail to reject}$ the null hypothesis.
