Z-test for testing population mean
In this tutorial we will discuss some numerical examples on one sample z test for population mean.
Example 1
The average cost of tuition and room and board at a small private liberal arts college is reported to be $8,500 per term, but a financial administrator believes that the average cost is lower. A study conducted using 350 small liberal arts colleges showed that the average cost per term is $8,445. The population standard deviation is $1,200. Let $\alpha= 0.05$. What is the test statistic for this test?
Solution
Let $X$ denote cost of tution, room and board at a small private liberal arts college. Given that $n = 350$, sample mean cost of tution, room and board at a small private liberal arts college is $\overline{x} = 8445$, the population standard deviation is $\sigma = 1200$.
Step 1 Hypothesis Testing Problem
The hypothesis testing problem is $H_0 : \mu = 8500$ against $H_1 : \mu < 8500$ ($\text{left-tailed}$)
Step 2 Test Statistic
The test statistic for testing above hypothesis testing problem is
$$ \begin{aligned} Z& =\frac{\overline{x} -\mu}{\sigma/\sqrt{n}}. \end{aligned} $$
The test statistic $Z$ follows $N(0,1)$ distribution.
Step 3 Significance Level
The significance level is $\alpha = 0.05$.
Step 4 Critical Value(s)
As the alternative hypothesis is $\text{left-tailed}$, the critical value of $Z$ $\text{is}$ $-1.64$ (from Normal Statistical Table).
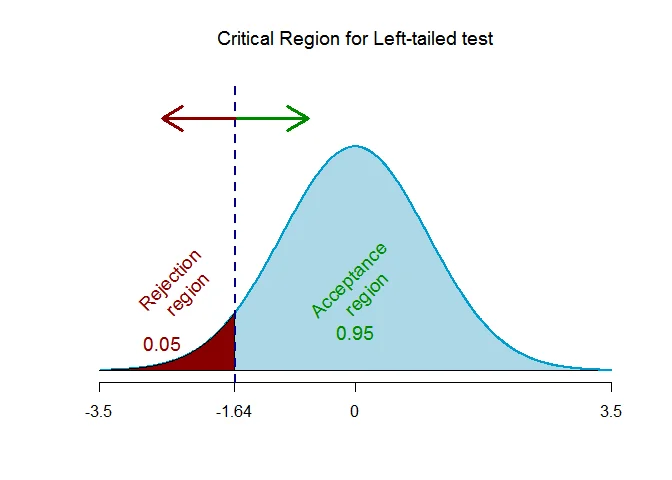
The rejection region (i.e. critical region) is $\text{Z < -1.64}$.
Step 5 Computation
The test statistic under the null hypothesis is
$$ \begin{aligned} Z_{obs}&=\frac{ \overline{x} -\mu_0}{\sigma/\sqrt{n}}\\ &= \frac{8445-8500}{1200/ \sqrt{350 }}\\ &= -0.857 \end{aligned} $$
Step 6 Decision (Traditional Approach)
The test statistic is $Z_{obs} =-0.857$ which falls $\text{outside}$ the critical region, we $\text{fail to reject}$ the null hypothesis at $\alpha = 0.05$ level of significance.
OR
Step 6 Decision ($p$-value Approach)
This is a $\text{left-tailed}$ test, so the p-value is the area to the $\text{left}$ of the test statistic ($Z_{obs}=-0.857$) is p-value = $0.1956$.
The p-value is $0.1956$ which is $\text{greater than}$ the significance level of $\alpha = 0.05$, we $\text{fail to reject}$ the null hypothesis at $\alpha =0.05$ level of significance.
Example 2
The health of the bear population in Yellowstone National Park is monitored by periodic measurements taken from anesthetized bears. A sample of 54 bears has a mean weight of 182.9 lb. Assuming that is $\sigma$ known to be 121.8 lb, use a 0.05 significance level to test the claim that the population mean of all such bear weights is greater than 150 lb.
Solution
Let $X$ denote weight of bear. Given that $n = 54$, sample mean weight of bear is $\overline{x} = 182.9$, the population standard deviation is $\sigma = 121.8$.
Step 1 Hypothesis Testing Problem
The hypothesis testing problem is $H_0 : \mu = 150$ against $H_1 : \mu > 150$ ($\text{right-tailed}$)
Step 2 Test Statistic
The test statistic for testing above hypothesis testing problem is
$$ \begin{aligned} Z& =\frac{\overline{x} -\mu}{\sigma/\sqrt{n}}. \end{aligned} $$
The test statistic $Z$ follows $N(0,1)$ distribution.
Step 3 Significance Level
The significance level is $\alpha = 0.05$.
Step 4 Critical Value(s)
As the alternative hypothesis is $\text{right-tailed}$, the critical value of $Z$ $\text{is}$ $1.64$ (from Normal Statistical Table).
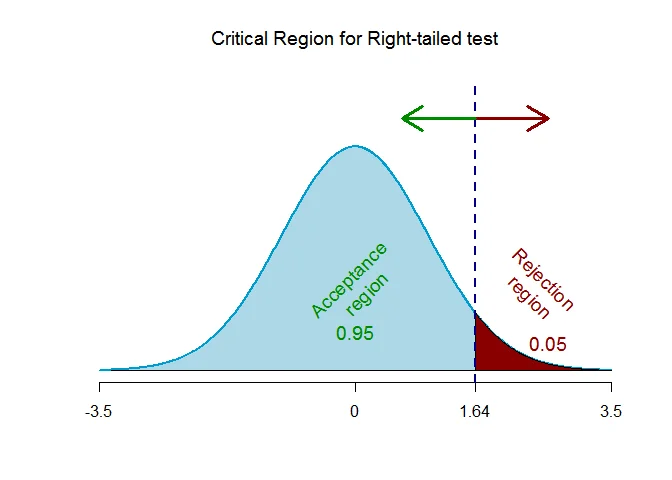
The rejection region (i.e. critical region) is $\text{Z > 1.64}$.
Step 5 Computation
The test statistic under the null hypothesis is
$$ \begin{aligned} Z_{obs}&=\frac{ \overline{x} -\mu_0}{\sigma/\sqrt{n}}\\ &= \frac{182.9-150}{121.8/ \sqrt{54 }}\\ &= 1.985 \end{aligned} $$
Step 6 Decision (Traditional Approach)
The test statistic is $Z_{obs} =1.985$ which falls $\text{inside}$ the critical region, we $\text{reject}$ the null hypothesis at $\alpha = 0.05$ level of significance.
OR
Step 6 Decision ($p$-value Approach)
This is a $\text{right-tailed}$ test, so the p-value is the area to the $\text{right}$ of the test statistic ($Z_{obs}=1.985$) is p-value = $0.0236$.
The p-value is $0.0236$ which is $\text{less than}$ the significance level of $\alpha = 0.05$, we $\text{reject}$ the null hypothesis at $\alpha =0.05$ level of significance.
Example 3
A company that makes cola drinks states that the mean caffeine content per 12 ounce bottle of cola is 40 milligrams. During the test it was found that a random sample of thirty 12-ounce bottles of cola has a mean caffeine content of 38.7 milligrams. The population standard deviation is 7.3 milligrams. At $\alpha = 0.01$ test the claim of the company.
Solution
Let $X$ denote caffeine content per 12 ounce bottle of cola. Given that $n = 30$, sample mean caffeine content per 12 ounce bottle of cola is $\overline{x} = 38.7$, the population standard deviation is $\sigma = 7.3$.
Step 1 Hypothesis Testing Problem
The hypothesis testing problem is $H_0 : \mu = 40$ against $H_1 : \mu \neq 40$ ($\text{two-tailed}$)
Step 2 Test Statistic
The test statistic for testing above hypothesis testing problem is
$$ \begin{aligned} Z& =\frac{\overline{x} -\mu}{\sigma/\sqrt{n}}. \end{aligned} $$
The test statistic $Z$ follows $N(0,1)$ distribution.
Step 3 Significance Level
The significance level is $\alpha = 0.01$.
Step 4 Critical Value(s)
As the alternative hypothesis is $\text{two-tailed}$, the critical values of $Z$ $\text{are}$ $-2.58$ and $2.58$ (from Normal Statistical Table).
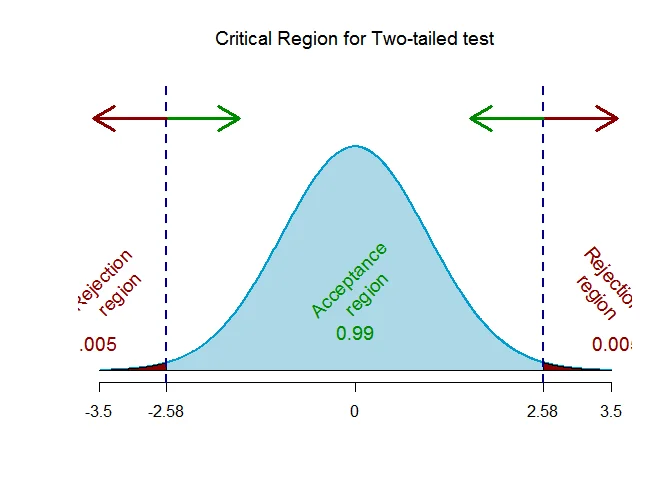
The rejection region (i.e. critical region) is $\text{Z < -2.58 or Z > 2.58}$.
Step 5 Computation
The test statistic under the null hypothesis is
$$ \begin{aligned} Z_{obs}&=\frac{ \overline{x} -\mu_0}{\sigma/\sqrt{n}}\\ &= \frac{38.7-40}{7.3/ \sqrt{30 }}\\ &= -0.975 \end{aligned} $$
Step 6 Decision (Traditional Approach)
The test statistic is $Z_{obs} =-0.975$ which falls $\text{outside}$ the critical region, we $\text{fail to reject}$ the null hypothesis at $\alpha = 0.01$ level of significance.
OR
Step 6 Decision ($p$-value Approach)
This is a $\text{two-tailed}$ test, so the p-value is the area to the $\text{extreme}$ of the test statistic ($Z_{obs}=-0.975$) is p-value = $0.3294$.
The p-value is $0.3294$ which is $\text{greater than}$ the significance level of $\alpha = 0.01$, we $\text{fail to reject}$ the null hypothesis at $\alpha =0.01$ level of significance.
