Z-Test for Proportion
In this tutorial we will discuss some numerical examples on one sample Z test for testing population proportion.
Example 1
An insurance company states that 90% of its claims are settled within 30 days. A consumer group selected a random sample of 75 of the company’s claims to test this statement. If the consumer group found that 55 of the claims were settled within 30 days, do they have sufficient reason to support their contention that fewer than 90% of the claims are settled within 30 days? Use 5% level of significance.
Solution
Given that $n = 75$, $X= 55$.
The sample proportion is
$$\hat{p}=\frac{X}{n}=\frac{55}{75}=0.733$$
Step 1 Hypothesis Testing Problem
The hypothesis testing problem is $H_0 : p = 0.9$ against $H_1 : p < 0.9$ ($\text{left-tailed}$)
Step 2 Test Statistic
The test statistic for testing above hypothesis testing problem is
$$ \begin{aligned} Z & = \frac{\hat{p} - p}{\sqrt{\frac{p(1-p)}{n}}} \end{aligned} $$
which follows $N(0,1)$ distribution.
Step 3 Significance Level
The significance level is $\alpha = 0.05$.
Step 4 Critical values
As the alternative hypothesis is $\textit{left-tailed}$, the critical value of $Z$ $\text{ is }$ $\text{-1.64}$.
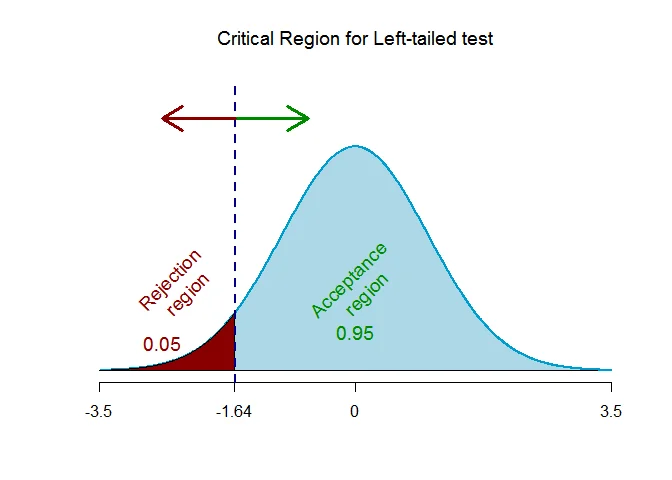
The rejection region (i.e. critical region) for the hypothesis testing problem is $\text{Z < -1.64}$.
Step 5 Computation
The test statistic is
$$ \begin{aligned} Z & = \frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\\ &= \frac{0.733-0.9}{\sqrt{\frac{0.9* (1-0.9)}{75}}}\\ & =-4.811 \end{aligned} $$
Step 6 Decision (Traditional approach)
The test statistic is $Z =-4.811$ which falls $inside$ the critical region, we $\text{reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value approach)
This is a $\text{left-tailed}$ test, so the p-value is the area to the left of the test statistic ($Z=-4.811$). Thus the $p$-value = $P(Z<-4.811) =0$.
The p-value is $0$ which is $\text{less than}$ the significance level of $\alpha = 0.05$, we $\text{reject}$ the null hypothesis.
Interpretation
There is sufficient reason to support their contention that fewer than 90% of the claims are settled within 30 days.
Example 2
An auditor for the U.S. Postal Service wants to examine its special two-day priority mail handling to determine the proportion of parcels that actually arrive within the promised two-day period. A randomly selected sample of 1600 such parcels is found to contain 1250 that were delivered on time. Does the sample data provide evidence to conclude that the percentage of on-time parcels is more than 75% (using $\alpha=0.01$)?
Solution
Given that $n = 1600$, $X= 1250$.
The sample proportion is
$$\hat{p}=\frac{X}{n}=\frac{1250}{1600}=0.781.$$
Step 1 Hypothesis Testing Problem
The hypothesis testing problem is $H_0 : p = 0.75$ against $H_1 : p > 0.75$ ($\text{right-tailed}$)
Step 2 Test Statistic
The test statistic for testing above hypothesis testing problem is
$$ \begin{aligned} Z & = \frac{\hat{p} - p}{\sqrt{\frac{p(1-p)}{n}}} \end{aligned} $$
which follows $N(0,1)$ distribution.
Step 3 Significance Level
The significance level is $\alpha = 0.01$.
Step 4 Critical values
As the alternative hypothesis is $\textit{right-tailed}$, the critical value of $Z$ $\text{ is }$ $\text{2.33}.$

The rejection region (i.e. critical region) for the hypothesis testing problem is $\text{Z > 2.33}$.
Step 5 Computation
The test statistic is
$$ \begin{aligned} Z & = \frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\\ &= \frac{0.781-0.75}{\sqrt{\frac{0.75* (1-0.75)}{1600}}}\\ & =2.887 \end{aligned} $$
Step 6 Decision (Traditional approach)
The test statistic is $Z =2.887$ which falls $inside$ the critical region, we $\text{reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value approach)
This is a $\text{right-tailed}$ test, so the p-value is the area to the left of the test statistic ($Z=2.887$). Thus the $p$-value = $P(Z<2.887) =0.0019$.
The p-value is $0.0019$ which is $\text{less than}$ the significance level of $\alpha = 0.01,$ we $\text{reject}$ the null hypothesis.
Interpretation
The sample data provide enough evidence at $\alpha=0.01$ level of significance to conclude that the percentage of on-time parcels is more than 75%.
Example 3
A survey by Men’s Health magazine stated that 14% of men said they used exercise to reduce stress. A random sample of 100 men was selected, and 10 said that they used exercise to relieve stress. Test the claim at $\alpha= 0.10$.
Solution
Given that $n = 100$, $X= 10$.
The sample proportion is
$$\hat{p}=\frac{X}{n}=\frac{10}{100}=0.1$$
Step 1 Hypothesis Testing Problem
The hypothesis testing problem is $H_0 : p = 0.14$ against $H_1 : p \neq 0.14$ ($\text{two-tailed}$)
Step 2 Test Statistic
The test statistic for testing above hypothesis testing problem is
$$ \begin{aligned} Z & = \frac{\hat{p} - p}{\sqrt{\frac{p(1-p)}{n}}} \end{aligned} $$
which follows $N(0,1)$ distribution.
Step 3 Significance Level
The significance level is $\alpha = 0.1$.
Step 4 Critical values
As the alternative hypothesis is $\textit{two-tailed}$, the critical value of $Z$ $\text{ are }$ $\text{-1.64 and 1.64}$.

The rejection region (i.e. critical region) for the hypothesis testing problem is $\text{Z < -1.64 or Z > 1.64}$.
Step 5 Computation
The test statistic is
$$ \begin{aligned} Z & = \frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\\ &= \frac{0.1-0.14}{\sqrt{\frac{0.14* (1-0.14)}{100}}}\\ & =-1.153 \end{aligned} $$
Step 6 Decision (Traditional approach)
The test statistic is $Z =-1.153$ which falls $outside$ the critical region, we $\text{fail to reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value approach)
This is a $\text{two-tailed}$ test, so the p-value is the area to the left of the test statistic ($Z=-1.153$). Thus the $p$-value = $P(Z<-1.153) =0.249$.
The p-value is $0.249$ which is $\text{greater than}$ the significance level of $\alpha = 0.1$, we $\text{fail to reject}$ the null hypothesis.
Interpretation
There is not sufficient evidence to say that the percentage of men who use exercise to reduce stress is not $14$%.
