Two sample Z test for means
In this tutorial we will discuss some numerical examples on two sample z test for testing difference between the means.
Example 1
An industrial engineer would like to determine whether there are more units produced on the night shift than on the day shift. Assume that the population standard deviation for the number of units produced on the day shift is 21 and is 28 on the night shift. A sample of 54 day shift workers showed that the mean number of units produced was 342. A sample of 60 night shift workers showed the mean number of units produced was 351. At the 0.05 significant level, is the average number of units produced on the night shift larger than the day shift?
Solution
Given that the sample size for day shift is $n_1 = 54$, and sample size for night shift is $n_2 = 60$. The average no. of units produced on the day shift is $\overline{x}_1= 342$, and the average no. of units produced on the night shift is $\overline{x}_2= 351$. The population standard deviation for the no. of units produced on the days shift is $\sigma_1 = 21$ and on the night shift is $\sigma_2 = 28$.
Step 1 State the hypothesis testing problem
We wish to test the hypothesis that the average number of units produced on the night shift ($\mu_2$) is larger than the day shift workers ($\mu_1$).
The hypothesis testing problem is
$H_0 : \mu_1 = \mu_2$ against $H_1 : \mu_1 < \mu_2$ ($\textit{left-tailed}$)
Step 2 Define test statistic
The test statistic for testing above hypothesis problem is
$$ \begin{aligned} Z=\frac{(\overline{x}_1 -\overline{x}_1)-(\mu_1 -\mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}. \end{aligned} $$
The test statistic $Z$ follows standard normal distribution $N(0,1)$.
Step 3 Specify the level of significance
The significance level is $\alpha = 0.05$.
Step 4 Determine the critical value
As the alternative hypothesis is $\textit{left-tailed}$, the critical value of $Z$ $\text{is}$ $\text{-1.64}$.
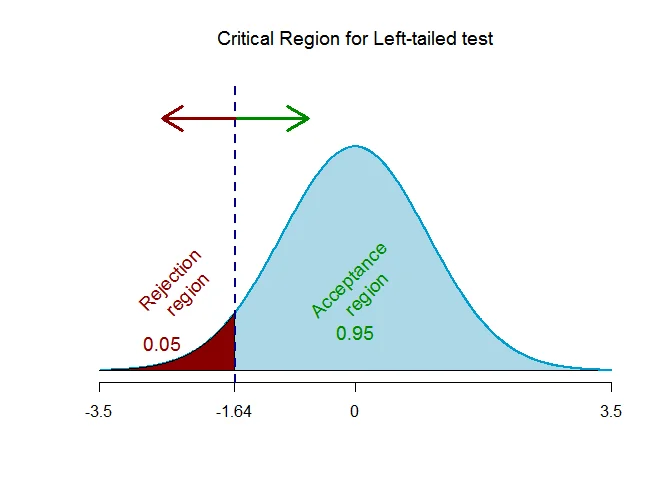
The rejection region (i.e. critical region) is $\text{Z < -1.64}$.
Step 5 Computation
The test statistic for testing above hypothesis under the null hypothesis is
$$ \begin{aligned} Z_{obs}&=\frac{(\overline{x}_1 -\overline{x}_1)-0}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}\\ &= \frac{342-351}{\sqrt{\frac{21^2}{54}+\frac{28^2}{60}}}\\ &= -1.953 \end{aligned} $$
Step 6 Decision (Traditional approach)
The rejection region (i.e. critical region) is $\text{Z < -1.64}$. The test statistic is $Z_{obs} =-1.953$ which falls $inside$ the critical region, we $\textit{reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value approach)
The test is $\text{left-tailed}$ test, so the p-value is the area to the $\text{left}$ of the test statistic ($Z_{obs}=-1.953$) is p-value = $0.0254$.
The p-value is $0.0254$ which is $\textit{less than}$ the significance level of $\alpha = 0.05$, we $\textit{reject}$ the null hypothesis.
Interpretation
There is enough evidence to support the alternative hypothesis.
The average number of units produced on the night shift is larger than number of units produced on the day shift.
Example 2
In a life testing problem, the mean life of 38 cells of a company A, was found to be 30 hours. The mean life of 35 cells of company B, was found to be 25 hours. The population standard deviations are 10.48 hours and 9.48 hours for company A and company B respectively. On the basis of this information, can it be inferred that company A’s product is significantly better than company B’s product?
Solution
Given that the sample size $n_1 = 38$, $n_2 = 35$, sample mean $\overline{x}_1= 30$, $\overline{x}_2= 25$, standard deviation $\sigma_1 = 10.48$ and $\sigma_2 = 9.48$.
Step 1 State the hypothesis testing problem
The hypothesis testing problem is
$H_0 : \mu_1 = \mu_2$ against $H_1 : \mu_1 > \mu_2$ ($\textit{right-tailed}$)
Step 2 Define test statistic
The test statistic is
$$ \begin{aligned} Z&=\frac{(\overline{x}_1 -\overline{x}_1)-(\mu_1 -\mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}. \end{aligned} $$
The test statistic $Z$ follows standard normal distribution $N(0,1)$.
Step 3 Specify the level of significance
The significance level is $\alpha = 0.05$.
Step 4 Determine the critical value
As the alternative hypothesis is $\textit{right-tailed}$, the critical value of $Z$ $\text{is}$ $\text{1.64}$.
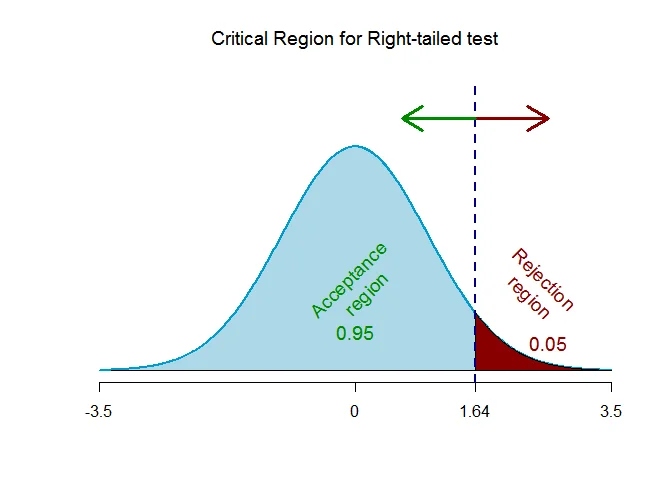
The rejection region (i.e. critical region) is $\text{Z > 1.64}$.
Step 5 Computation
The test statistic for testing above hypothesis under the null hypothesis is
$$ \begin{aligned} Z_{obs}&=\frac{(\overline{x}_1 -\overline{x}_1)-0}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}\\ &= \frac{30-25}{\sqrt{\frac{10.48^2}{38}+\frac{9.48^2}{35}}}\\ &= 2.14 \end{aligned} $$
Step 6 Decision (Traditional approach)
The rejection region (i.e. critical region) is $\text{Z > 1.64}$. The test statistic is $Z_{obs} =2.14$ which falls $inside$ the critical region, we $\textit{reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value approach)
The test is $\text{right-tailed}$ test, so the p-value is the area to the $\text{right}$ of the test statistic ($Z_{obs}=2.14$) is p-value = $0.0162$.
The p-value is $0.0162$ which is $\textit{less than}$ the significance level of $\alpha = 0.05$, we $\textit{reject}$ the null hypothesis.
Interpretation
There is enough evidence to support the alternative hypothesis at $0.05$ level of significance.
Company A’s product is significantly better than that of company B’s product.
Example 3
Two kinds of thread are being compared for tensile strength. Fourty pieces of each type of thread are tested under similar conditions. Brand A has an average tensile strength of 81.6 kilograms with a standard deviation of 4.5 kilograms, while brand B had an average tensile strength of 84.5 kilograms with a standard deviation of 5.1 kilograms.
Is there a significant difference between the average tensile strength of the threads from two brands?
Solution
Given that the sample size $n_1 = 40$, $n_2 = 40$, sample mean $\overline{x}_1= 82.9$, $\overline{x}_2= 84.5$, standard deviation $\sigma_1 = 5.4$ and $\sigma_2 = 5.8$.
Step 1 State the hypothesis testing problem
The hypothesis testing problem is
$H_0 : \mu_1 = \mu_2$ against $H_1 : \mu_1 \neq \mu_2$ ($\textit{two-tailed}$)
Step 2 Define test statistic
The test statistic is
$$ \begin{aligned} Z=\frac{(\overline{x}_1 -\overline{x}_1)-(\mu_1 -\mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}. \end{aligned} $$
The test statistic $Z$ follows standard normal distribution $N(0,1)$.
Step 3 Specify the level of significance
The significance level is $\alpha = 0.05$.
Step 4 Determine the critical value
As the alternative hypothesis is $\textit{two-tailed}$, the critical value of $Z$ $\text{are}$ $\text{-1.96 and 1.96}$.
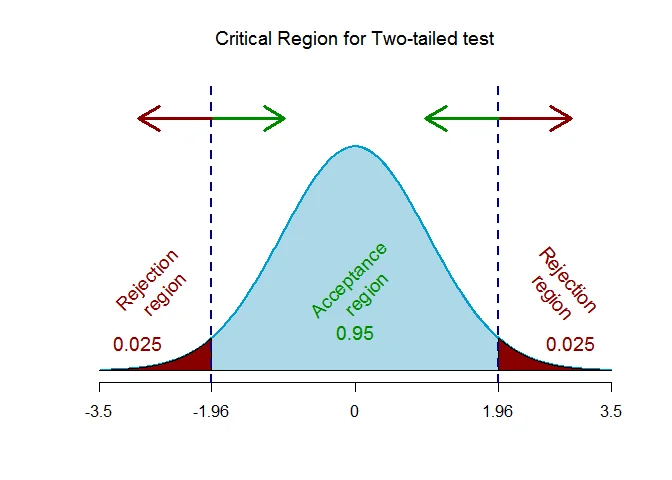
The rejection region (i.e. critical region) is $\text{Z < -1.96 or Z > 1.96}$.
Step 5 Computation
The test statistic for testing above hypothesis under the null hypothesis is
$$ \begin{aligned} Z_{obs}&=\frac{(\overline{x}_1 -\overline{x}_1)-0}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}\\ &= \frac{82.9-84.5}{\sqrt{\frac{5.4^2}{40}+\frac{5.8^2}{40}}}\\ &= -1.277 \end{aligned} $$
Step 6 Decision (Traditional approach)
The rejection region (i.e. critical region) is $\text{Z < -1.96 or Z > 1.96}$. The test statistic is $Z_{obs} =-1.277$ which falls $outside$ the critical region, we $\textit{fail to reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value approach)
The test is $\text{two-tailed}$ test, so the p-value is the area to the $\text{extreme}$ of the test statistic ($Z_{obs}=-1.277$) is p-value = $0.2016$.
The p-value is $0.2016$ which is $\textit{greater than}$ the significance level of $\alpha = 0.05$, we $\textit{fail to reject}$ the null hypothesis.
Interpretation
There is no significant difference between the average tensile strength of the threads from two brands.
