Negative Binomial Distribution Calculator
Use Negative Binomial Distribution Calculator to find the probability and cumulative probabilities for negative binomial random variable given the number of successes ($r$) and probability of success ($p$).
Calculator
| Negative Binomial Distribution Calculator | |
|---|---|
| Number of successes (r): | |
| Number of failures (x): | |
| Probability of success (p): | |
| Negative Probability Calculator Result | |
| Probability : P(X = x) | |
| Cumulative Probability : P(X ≤ x) | |
| Cumulative Probability : P(X < x) | |
| Cumulative Probability : P(X ≥ x) | |
| Cumulative Probability : P(X > x) | |
How to use Negative Binomial Distribution Calculator?
Step 1 - Enter the number of successes (r)
Step 2 - Enter the number of failures (x)
Step 3 - Enter the probabilities of success (p)
Step 4 - Click on “Calculate” for negative probability calculation
Step 5 - Calculate Probability
Step 6 - Calculate different cumulative probabilities
Negative Binomial Distribution Definition
A discrete random variable $X$ is said to have Negative Binomial distribution with parameter $r$ and $p$ if its probability mass function is
$$ \begin{aligned} P(X=x)&= \binom{x+r-1}{r-1} p^{r} q^{x},\\ & \quad \quad x=0,1,2,\ldots; r=1,2,\ldots\\ & \quad\quad \qquad 0<p, q<1, p+q=1. \end{aligned} $$
where
- $r =$ number of successes,
- $x =$ number of failures before $r^{th}$ success,
- $p =$ probability of success,
- $q = 1- p =$ probability of failures.
Mean of Negative Binomial Distribution
The mean of negative binomial distribution is
$E(X)=\dfrac{rq}{p}$.
Variance of Negative Binomial Distribution
The variance of negative binomial distribution is
$V(X)=\dfrac{rq}{p^2}$.
For negative binomial distribution $V(X)> E(X)$, i.e., variance > mean.
MGF of Negative Binomial Distribution
The MGF of negative binomial distribution is
$M_X(t)=\big(Q-Pe^{t}\big)^{-r}$.
CGF of Negative Binomial Distribution
The CGF of negative binomial distribution is
$K_X(t)=-r\log_e(Q-Pe^t)$.
Characteristics Function of negative binomial distribution
The characteristics function of negative binomial distribution is
$\phi_X(t) = p^r (1-qe^{it})^{-r}$.
Lets check out few of the examples with step by step explanation on negative binomial distribution
Negative Binomial Distribution Example 1
A large lot of tires contains 5% defectives. 4 tires are to be chosen for a car.
a. Find the probability that you find 2 defective tires before 4 good ones.
b. Find the probability that you find at most 2 defective tires before 4 good ones.
c. Find the mean and variance of the number of defective tires you find before finding 4 good tires.
Solution
Let $X$ denote the number of defective tires you find before you find 4 good tires. A large lot of tires contains 5% defectives. So the probability of good tire is $p=0.95$.
The random variable $X\sim NB(4, 0.95)$.
using Negative Binomial Distribution Calculator, pmf is calculated as
The probability mass function of $X$ is
$$ \begin{aligned} P(X=x)&= \binom{x+4-1}{x} (0.95)^{4} (0.05)^{x},\quad x=0,1,2,\ldots\\ &= \binom{x+3}{x} (0.95)^{4} (0.05)^{x},\quad x=0,1,2,\ldots \end{aligned} $$
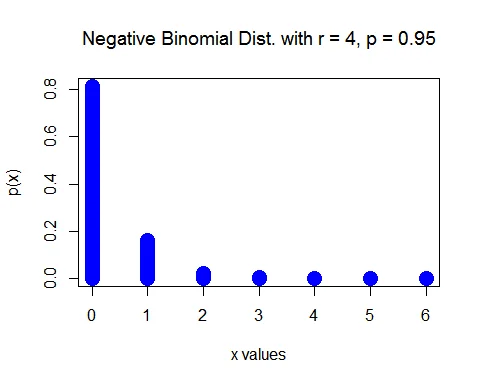
a. The probability that you find 2 defective tires before 4 good tires is
$$ \begin{aligned} P(X=2)&= \binom{2+3}{2} (0.95)^{4} (0.05)^{2}\\ &= \binom{5}{2} (0.8145)\times (0.0025)\\ &= 10*(0.00204)\\ &= 0.0204 \end{aligned} $$
b. The probability that you at most 2 defective tires before 4 good tires is
$$ \begin{aligned} P(X\leq 2)&=\sum_{x=0}^{2}P(X=x)\\ &= P(X=0)+P(X=1)+P(X=2)\\ &= \binom{0+3}{0} (0.95)^{4} (0.05)^{0}+\binom{1+3}{1} (0.95)^{4} (0.05)^{1}\\ &\quad +\binom{2+3}{2} (0.95)^{4} (0.05)^{2}\\ &= 1*(0.8145)+4*(0.04073)+10*(0.00204)\\ &= 0.8145+0.1629+0.0204\\ &=0.9978 \end{aligned} $$
c. The mean of the number of defective tires you find before finding 4 good tires is
$$ \begin{aligned} E(X) &= \frac{rq}{p}\\ &= \frac{4*0.05}{0.95}\\ &= 0.2105. \end{aligned} $$
The variance of the number of defective tires you find before finding 4 good tires is
$$ \begin{aligned} V(X) &= \frac{rq}{p^2}\\ &= \frac{4*0.05}{0.95^2}\\ &= 0.2216. \end{aligned} $$
Negative Binomial Distribution Calculator Example 2
The probability of male birth is 0.5. A couple wishes to have children until they have exactly two female children in their family.
a. Write the probability distribution of $X$, the number of male children before two female children.
b. What is the probability that the family has four children?
c. What is the probability that the family has at most four children?
d. What is the expected number of male children this family have?
e. What is the expected number of children this family have?
Solution
A couple wishes to have children until they have exactly two female children in their family.
Birth of female child is consider as success and birth of male child is consider as failure. The probability of male birth is $q=0.5$. So the probability of female birth is $p=1-q=0.5$. The number of female children (successes) $r=2$.
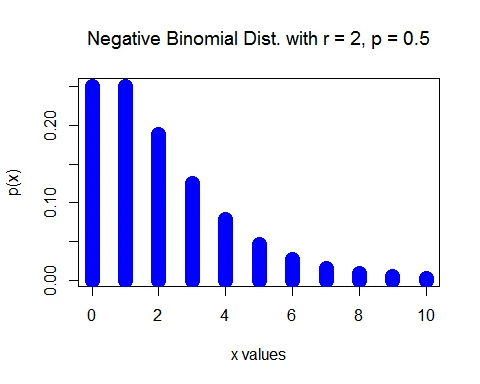
Here $X$ denote the number of male children before two female children. Then the random variable $X$ follows a negative binomial distribution $NB(2,0.5)$.
using negative probability calculator, probabilities are calculated as below :
a. The probability distribution of $X$ (number of male children before two female children) is
$$ \begin{aligned} P(X=x)&= \binom{x+2-1}{x} (0.5)^{2} (0.5)^{x},\quad x=0,1,2,\ldots\\ &= \binom{x+1}{x} (0.5)^{2} (0.5)^{x},\quad x=0,1,2,\ldots \end{aligned} $$
b. The family has four children means 2 male and 2 female. Thus probability that a family has four children is same as probability that a family has 2 male children before 2 female children.
$$ \begin{aligned} P(X=2) & = \frac{(2+1)!}{1!2!}(0.5)^{2}(0.5)^{2} \\ & = 0.1875 \end{aligned} $$
c. The family has at the most four children means $X$ is less than or equal to 2. Thus, the probability that a family has at the most four children is
$$ \begin{aligned} P(X\leq 2) & = \sum_{x=0}^{2} P(X=x)\\ & = p(0) + p(1) + p(2)\\ & = 0.25+ 0.25+0.1875\\ &= 0.6875 \end{aligned} $$
where
$$ \begin{aligned} p(0) & = \frac{(0+1)!}{1!0!}(0.5)^{2}(0.5)^{0}\\ & = 0.25. \end{aligned} $$
$$ \begin{aligned} p(1) & = \frac{(1+1)!}{1!1!}(0.5)^{2}(0.5)^{1}\\ & = 0.25. \end{aligned} $$
$$ \begin{aligned} p(2) & = \frac{(2+1)!}{1!2!}(0.5)^{2}(0.5)^{2}\\ & = 0.1875. \end{aligned} $$
d. The expected number of male children is
$$ \begin{aligned} E(X)& = \frac{rq}{p}\\ & = \frac{2\times0.5}{0.5}\\ & = 2 \end{aligned} $$
e. The expected number of children is
$$ \begin{aligned} E(X+2)& = E(X) + 2\\ &= 2+2. \end{aligned} $$
Conclusion
Hope you like and find above article on Negative Binomial Distribution Calculator with step by step guide with various numerical examples helpfule and educational.