Negative Binomial Distribution
In this tutorial, we will provide you step by step solution to some numerical examples on negative binomial distribution to make sure you understand the negative binomial distribution clearly and correctly.
Definition of Negative Binomial Distribution
A discrete random variable $X$ is said to have negative binomial distribution if its p.m.f. is given by
$$ \begin{aligned} P(X=x)&= \binom{x+r-1}{r-1} p^{r} q^{x},\\ & \quad \quad x=0,1,2,\ldots; r=1,2,\ldots\\ & \quad\quad \qquad 0<p, q<1, p+q=1. \end{aligned} $$
Mean of Negative Binomial Distribution
The mean of negative binomial distribution is $E(X)=\dfrac{rq}{p}$.
Variance of Negative Binomial Distribution
The variance of negative binomial distribution is $V(X)=\dfrac{rq}{p^2}$.
Example 1
A large lot of tires contains 5% defectives. 4 tires are to be chosen for a car.
a. Find the probability that you find 2 defective tires before 4 good ones.
b. Find the probability that you find at most 2 defective tires before 4 good ones.
c. Find the mean and variance of the number of defective tires you find before finding 4 good tires.
Solution
Let $X$ denote the number of defective tires you find before you find 4 good tires. A large lot of tires contains 5% defectives. So the probability of good tire is $p=0.95$.
The random variable $X\sim NB(4, 0.95)$.
The probability mass function of $X$ is
$$ \begin{aligned} P(X=x)&= \binom{x+4-1}{x} (0.95)^{4} (0.05)^{x},\quad x=0,1,2,\ldots\\ &= \binom{x+3}{x} (0.95)^{4} (0.05)^{x},\quad x=0,1,2,\ldots \end{aligned} $$
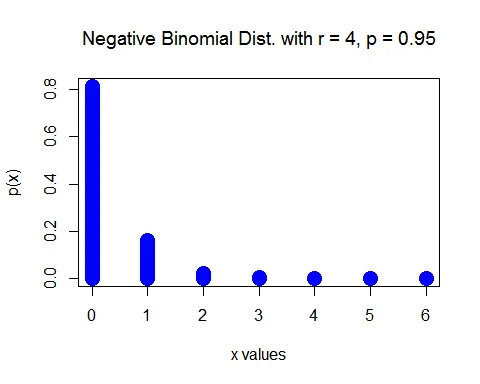
a. The probability that you find 2 defective tires before 4 good tires is
$$ \begin{aligned} P(X=2)&= \binom{2+3}{2} (0.95)^{4} (0.05)^{2}\\ &= \binom{5}{2} (0.8145)\times (0.0025)\\ &= 10*(0.00204)\\ &= 0.0204 \end{aligned} $$
b. The probability that you at most 2 defective tires before 4 good tires is
$$ \begin{aligned} P(X\leq 2)&=\sum_{x=0}^{2}P(X=x)\\ &= P(X=0)+P(X=1)+P(X=2)\\ &= \binom{0+3}{0} (0.95)^{4} (0.05)^{0}+\binom{1+3}{1} (0.95)^{4} (0.05)^{1}\\ &\quad +\binom{2+3}{2} (0.95)^{4} (0.05)^{2}\\ &= 1*(0.8145)+4*(0.04073)+10*(0.00204)\\ &= 0.8145+0.1629+0.0204\\ &=0.9978 \end{aligned} $$
c. The mean of the number of defective tires you find before finding 4 good tires is
$$ \begin{aligned} E(X) &= \frac{rq}{p}\\ &= \frac{4*0.05}{0.95}\\ &= 0.2105. \end{aligned} $$
The variance of the number of defective tires you find before finding 4 good tires is
$$ \begin{aligned} V(X) &= \frac{rq}{p^2}\\ &= \frac{4*0.05}{0.95^2}\\ &= 0.2216. \end{aligned} $$
Example 2
The probability of male birth is 0.5. A couple wishes to have children until they have exactly two female children in their family.
a. Write the probability distribution of $X$, the number of male children before two female children.
b. What is the probability that the family has four children?
c. What is the probability that the family has at most four children?
d. What is the expected number of male children this family have?
e. What is the expected number of children this family have?
Solution
A couple wishes to have children until they have exactly two female children in their family.
Birth of female child is consider as success and birth of male child is consider as failure. The probability of male birth is $q=0.5$. So the probability of female birth is $p=1-q=0.5$. The number of female children (successes) $r=2$.
Here $X$ denote the number of male children before two female children. Then the random variable $X$ follows a negative binomial distribution $NB(2,0.5)$.
a. The probability distribution of $X$ (number of male children before two female children) is
$$ \begin{aligned} P(X=x)&= \binom{x+2-1}{x} (0.5)^{2} (0.5)^{x},\quad x=0,1,2,\ldots\\ &= \binom{x+1}{x} (0.5)^{2} (0.5)^{x},\quad x=0,1,2,\ldots \end{aligned} $$
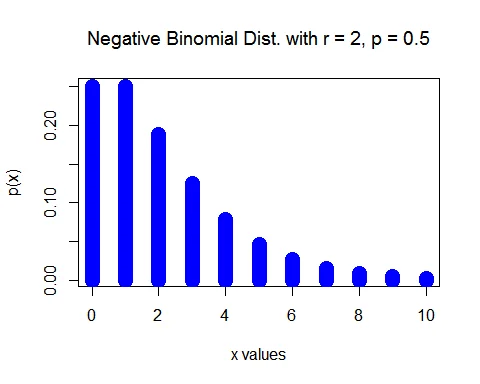
b. The family has four children means 2 male and 2 female. Thus probability that a family has four children is same as probability that a family has 2 male children before 2 female children.
$$ \begin{aligned} P(X=2) & = \frac{(2+1)!}{1!2!}(0.5)^{2}(0.5)^{2} \\ & = 0.1875 \end{aligned} $$
c. The family has at the most four children means $X$ is less than or equal to 2. Thus, the probability that a family has at the most four children is
$$ \begin{aligned} P(X\leq 2) & = \sum_{x=0}^{2} P(X=x)\\ & = p(0) + p(1) + p(2)\\ & = 0.25+ 0.25+0.1875\\ &= 0.6875 \end{aligned} $$
where
$$ \begin{aligned} p(0) & = \frac{(0+1)!}{1!0!}(0.5)^{2}(0.5)^{0}\\ & = 0.25. \end{aligned} $$
$$ \begin{aligned} p(1) & = \frac{(1+1)!}{1!1!}(0.5)^{2}(0.5)^{1}\\ & = 0.25. \end{aligned} $$
$$ \begin{aligned} p(2) & = \frac{(2+1)!}{1!2!}(0.5)^{2}(0.5)^{2}\\ & = 0.1875. \end{aligned} $$
d. The expected number of male children is
$$ \begin{aligned} E(X)& = \frac{rq}{p}\\ & = \frac{2\times0.5}{0.5}\\ & = 2 \end{aligned} $$
e. The expected number of children is
$$ \begin{aligned} E(X+2)& = E(X) + 2\\ &= 2+2. \end{aligned} $$
