Poisson distribution
In this tutorial, we will provide you step by step solution to some numerical examples on Poisson distribution to make sure you understand the Poisson distribution clearly and correctly.
Definition of Poisson Distribution
A discrete random variable $X$ is said to have Poisson distribution with parameter $\lambda$ if its probability mass function is
$$ \begin{equation*} P(X=x)= \left\{ \begin{array}{ll} \frac{e^{-\lambda}\lambda^x}{x!} , & \hbox{$x=0,1,2,\cdots; \lambda>0$;} \\ 0, & \hbox{Otherwise.} \end{array} \right. \end{equation*} $$
Mean of Poisson Distribution
The expected value of Poisson random variable is $E(X)=\lambda$.
Variance of Poisson Distribution
The variance of Poisson random variable is $V(X) =\lambda$.
Example 1
A book contains 500 pages. If there are 200 typing errors randomly distributed throughout the book, use the Poisson distribution to determine the probability that a page contains
a. exactly 3 errors,
b. at least 3 errors,
c. at most 2 errors,
d. 2 or more errors but less than 5 errors.
Solution
A book contains 500 pages and there are 200 typing errors randomly distributed throughout the book.
The average no. of typing errors per page $=\lambda =\frac{200}{500}= 0.4$.
The random variable $X$ is no. of typing errors per page. $X\sim P(0.4)$.
The probability mass function of Poisson distribution with $\lambda =0.4$ is
$$ \begin{aligned} P(X=x) &= \frac{e^{-0.4}(0.4)^x}{x!},\; x=0,1,2,\cdots \end{aligned} $$
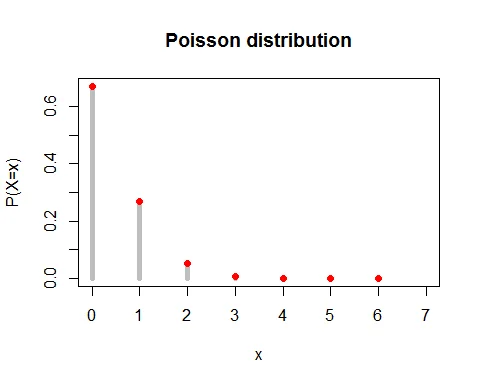
a. The probability that a page contains exactly 3 errors is
$$ \begin{aligned} P(X=3) &= \frac{e^{-0.4}0.4^{3}}{3!}\\ &= 0.0072 \end{aligned} $$
b. The probability that a page contains at least 3 errors is
$$ \begin{aligned} P(X\geq3) &= 1- P(X\leq 2)\\ &= 1- \sum_{x=0}^{2}P(X=x)\\ &= 1- \big[P(X=0) + P(X=1) + P(X=2)\big]\\ &= 1- \bigg[ \frac{e^{-0.4}0.4^{0}}{0!}+ \frac{e^{-0.4}0.4^{1}}{1!}+ \frac{e^{-0.4}0.4^{2}}{2!}\bigg]\\ &= 1-\big(0.6703+0.2681+0.0536\big)\\ &= 1-0.992\\ &= 0.008 \end{aligned} $$
c. The probability that a page contains at most 2 errors is
$$ \begin{aligned} P(X\leq2) &= \sum_{x=0}^{2}P(X=x)\\ &= P(X=0) + P(X=1) + P(X=2)\\ &= \frac{e^{-0.4}0.4^{0}}{0!}+ \frac{e^{-0.4}0.4^{1}}{1!}+ \frac{e^{-0.4}0.4^{2}}{2!}\\ &= 0.6703+0.2681+0.0536\\ &= 0.992 \end{aligned} $$
d. The probability that a page contains 2 or more errors but less than 5 errors is
$$ \begin{aligned} P(2\leq X< 5) &=P(2\leq X\leq 4)\\ &=P(X=2)+P(X=3)+P(X=4)\\ &= \frac{e^{-0.4}0.4^{2}}{2!}+\frac{e^{-0.4}0.4^{3}}{3!}+\frac{e^{-0.4}0.4^{4}}{4!}\\ &= 0.0536+0.0072+0.0007\\ &= 0.0615 \end{aligned} $$
Example 2
Suppose that in a certain area there are on average 5 traffic accidents per month. Find the probability of
a. 4 accidents in a given month,
b. at least 2 accidents in a given month,
c. at most 2 accidents in a given month.
Solution
The average no. of traffic accidents per month $=\lambda = 5$.
The random variable $X$ is no. of traffic accidents per month. $X\sim P(5)$.
The probability mass function of Poisson distribution with $\lambda =5$ is
$$ \begin{aligned} P(X=x) &= \frac{e^{-5}(5)^x}{x!},\; x=0,1,2,\cdots \end{aligned} $$
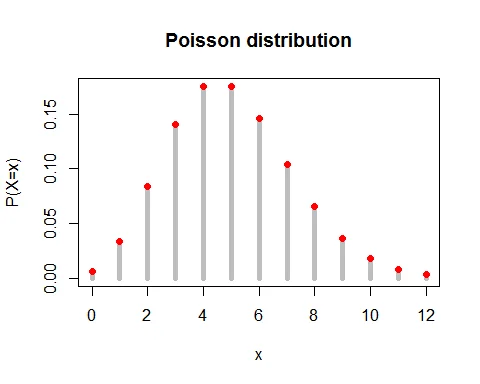
a. The probability of $4$ accidents in a given month is
$$ \begin{aligned} P(X=4) &= \frac{e^{-5}5^{4}}{4!}\\ &= 0.1755 \end{aligned} $$
b. The probability of at least 2 accidents in a given month is
$$ \begin{aligned} P(X\geq2) &= 1- P(X\leq 1)\\ &= 1- \sum_{x=0}^{1}P(X=x)\\ &= 1- \big[P(X=0) + P(X=1)\big]\\ &= 1- \bigg[ \frac{e^{-5}5^{0}}{0!}+ \frac{e^{-5}5^{1}}{1!}\bigg]\\ &= 1-\big(0.0067+0.0337\big)\\ &= 1-0.0404\\ &= 0.9596 \end{aligned} $$
c. The probability of at most 2 traffic accidents is
$$ \begin{aligned} P(X\leq2) &= \sum_{x=0}^{2}P(X=x)\\ &= P(X=0) + P(X=1) + P(X=2)\\ &= \frac{e^{-5}5^{0}}{0!}+ \frac{e^{-5}5^{1}}{1!}+ \frac{e^{-5}5^{2}}{2!}\\ &= 0.0067+0.0337+0.0842\\ &= 0.1246 \end{aligned} $$
Hope this article helps you understand how to solve the numerical problems on Poisson distribution.
