Poisson Distribution
Poisson distribution helps to describe the probability of occurrence of a number of events in some given time interval or in a specified region. The time interval may be of any length, such as a minutes, a day, a week etc.
Definition of Poisson Distribution
A discrete random variable $X$ is said to have Poisson distribution with parameter $\lambda$ if its probability mass function is
$$ \begin{equation*} P(X=x)= \left\{ \begin{array}{ll} \frac{e^{-\lambda}\lambda^x}{x!} , & \hbox{$x=0,1,2,\cdots; \lambda>0$;} \\ 0, & \hbox{Otherwise.} \end{array} \right. \end{equation*} $$
The variate $X$ is called Poisson variate and $\lambda$ is called the parameter of Poisson distribution.
In notation, it can be written as $X\sim P(\lambda)$.
Key features of Poisson Distribution
- Let X denote the number of times an event occurs in a given interval. The interval can be time, area, volume or distance.
- The probability of occurrence of an event is same for each interval.
- The occurrence of an event in one interval is independent of the occurrence in other interval.
Poisson distribution as a limiting form of binomial distribution
In binomial distribution if $n\to \infty$, $p\to 0$ such that $np=\lambda$ (finite) then binomial distribution tends to Poisson distribution
Proof
Let $X\sim B(n,p)$ distribution. Then the probability mass function of $X$ is
$$ \begin{equation*} P(X=x)= \left\{ \begin{array}{ll} \binom{n}{x} p^x q^{n-x}, & \hbox{$x=0,1,2,\cdots, n; 0<p<1; q=1-p$} \\ 0, & \hbox{Otherwise.} \end{array} \right. \end{equation*} $$
Taking the $\lim$ as $n\to \infty$ and $p\to 0$, we have
$$ \begin{eqnarray*} P(x) &=& \lim_{n\to\infty \atop{p\to 0}} \binom{n}{x} p^x q^{n-x} \\ &=& \lim_{n\to\infty \atop{p\to 0}} \frac{n!}{(n-x)!x!} p^x q^{n-x} \\ &=& \lim_{n\to\infty \atop{p\to 0}} \frac{n(n-1)(n-2)\cdots (n-x+1)}{x!} p^x q^{n-x} \\ &=& \lim_{n\to\infty \atop{p\to 0}} \frac{n^x(-\frac{1}{n})(1-\frac{2}{n})\cdots (1-\frac{x-1}{n})}{x!} p^x (1-p)^{n-x} \\ &=& \lim_{n\to\infty \atop{p\to 0}} \frac{(np)^x(1-\frac{1}{n})(1-\frac{2}{n})\cdots (1-\frac{x-1}{n})}{x!}(1-p)^{n-x} \\ &=& \lim_{n\to\infty \atop{p\to 0}} \frac{\lambda^x}{x!}\big(1-\frac{1}{n}\big)\big(1-\frac{2}{n}\big)\cdots \big(1-\frac{x-1}{n}\big)\big(1-\frac{\lambda}{n}\big)^{n-x} \\ &=& \frac{\lambda^x}{x!}\lim_{n\to\infty }\bigg[\big(1-\frac{\lambda}{n}\big)^{-n/\lambda}\bigg]^{-\lambda}\big(1-\frac{\lambda}{n}\big)^{-x} \\ &=& \frac{\lambda^x}{x!}e^{-\lambda} (1)^{-x}\qquad (\because \lim_{n\to \infty}\big(1-\frac{\lambda}{n}\big)^{-n/\lambda}=e)\\ &=& \frac{e^{-\lambda}\lambda^x}{x!},\;\; x=0,1,2,\cdots; \lambda>0. \end{eqnarray*} $$
Clearly, $P(x)\geq 0$ for all $x\geq 0$, and
$$ \begin{eqnarray*} \sum_{x=0}^\infty P(x) &=& \sum_{x=0}^\infty \frac{e^{-\lambda}\lambda^x}{x!} \\ &=& e^{-\lambda}\sum_{x=0}^\infty \frac{\lambda^x}{x!} \\ &=& e^{-\lambda}\bigg(1+\frac{\lambda}{1!}+\frac{\lambda^2}{2!}+\cdots + \bigg)\\ &=& e^{-\lambda}e^{\lambda}=1. \end{eqnarray*} $$
Hence, $P(x)$ is a legitimate probability mass function.
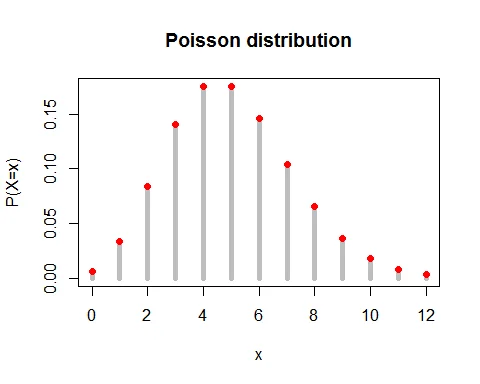
Graph of Poisson Distribution
Following graph shows the probability mass function of Poisson distribution with parameter $\lambda = 5$.
Mean of Poisson Distribution
The expected value of Poisson random variable is $E(X)=\lambda$.
Proof
The expected value of Poisson random variable is
$$ \begin{eqnarray*} E(X) &=& \sum_{x=0}^\infty x\cdot P(X=x)\\ &=& \sum_{x=0}^\infty x\cdot \frac{e^{-\lambda}\lambda^x}{x!}\\ &=& 0 +\lambda e^{-\lambda}\sum_{x=1}^\infty \frac{\lambda^{x-1}}{(x-1)!}\\ &=& \lambda e^{-\lambda}\bigg(1+\frac{\lambda}{1!}+\frac{\lambda^2}{2!}+\cdots + \bigg)\\ &=& \lambda e^{-\lambda}e^{\lambda} \\ &=& \lambda. \end{eqnarray*} $$
Variance of Poisson Distribution
The variance of Poisson random variable is $V(X) =\lambda$.
Proof
The variance of random variable $X$ is given by
$$ V(X) = E(X^2) - [E(X)]^2 $$
Let us find the expected value $X^2$.
$$ \begin{eqnarray*} E(X^2) & = & E[X(X-1)]+ E(X)\\ &=& \sum_{x=0}^\infty x(x-1)\cdot P(X=x)+\lambda\\ &=& \sum_{x=0}^\infty x(x-1)\cdot \frac{e^{-\lambda}\lambda^x}{x!} +\lambda\\ &=& 0 +0+\lambda^2 e^{-\lambda}\sum_{x=2}^\infty \frac{\lambda^{x-2}}{(x-2)!}+\lambda\\ &=& \lambda^2 e^{-\lambda}\bigg(1+\frac{\lambda}{1!}+\frac{\lambda^2}{2!}+\cdots + \bigg)+\lambda\\ &=& \lambda^2 e^{-\lambda}e^{\lambda} = \lambda^2+\lambda. \end{eqnarray*} $$
Thus, variance of Poisson random variable is
$$ \begin{eqnarray*} V(X) &=& E(X^2) - [E(X)]^2\\ &=& \lambda^2+\lambda-\lambda^2\\ &=& \lambda. \end{eqnarray*} $$
For Poisson distribution, Mean = Variance = $\lambda$.
Moment Generating Funtion of Poisson Distribution
The moment generating function of Poisson distribution is $M_X(t)=e^{\lambda(e^t-1)}, t \in R$.
Proof
The moment generating function of Poisson random variable $X$ is
$$ \begin{eqnarray*} M_X(t) &=& E(e^{tx}) \\ &=& \sum_{x=0}^\infty e^{tx} \frac{e^{-\lambda}\lambda^x}{x!}\\ &=& e^{-\lambda}\sum_{x=0}^\infty \frac{(\lambda e^{t})^x}{x!}\\ &=& e^{-\lambda}\cdot e^{\lambda e^t}\\ &=& e^{\lambda(e^t-1)}, \; t\in R. \end{eqnarray*} $$
Moments of Poisson distribution from MGF
The moments of Poisson distribution can also be obtained from moment generating function.
The $r^{th}$ moment of Poisson random variable is given by
$$ \begin{equation*} \mu_r^\prime=\bigg[\frac{d^r M_X(t)}{dt^r}\bigg]_{t=0}. \end{equation*} $$
Proof
The moment generating function of Poisson distribution is $M_X(t) =e^{\lambda(e^t-1)}$.
Differentiating $M_X(t)$ w.r.t. $t$
$$ \begin{equation}\label{p11} \frac{d M_X(t)}{dt}= e^{\lambda(e^t-1)}(\lambda e^{t}). \end{equation} $$
Putting $t=0$, we get
$$ \begin{eqnarray*} \mu_1^\prime &=& \bigg[\frac{d M_X(t)}{dt}\bigg]_{t=0} \\ &=& \bigg[e^{\lambda(e^t-1)}(\lambda e^{t})\bigg]_{t=0}\\ &=& \lambda = \text{ mean }. \end{eqnarray*} $$
Again differentiating \eqref{p11} w.r.t. $t$, we get
$$ \begin{equation*} \frac{d^2 M_X(t)}{dt^2}= e^{\lambda(e^t-1)}(\lambda e^{t})+(\lambda e^t)e^{\lambda(e^t-1)}(\lambda e^{t}). \end{equation*} $$
Putting $t=0$, we get
$$ \begin{eqnarray*} \mu_2^\prime &=& \bigg[\frac{d^2 M_X(t)}{dt^2}\bigg]_{t=0} \\ &=& \lambda+\lambda^2. \end{eqnarray*} $$
Hence,
$$ \begin{equation*} \text{Variance }=\mu_2 = \mu_2^\prime - (\mu_1^\prime)^2=\lambda+\lambda^2-\lambda^2=\lambda. \end{equation*} $$
Characteristics Funtion of Poisson Distribution
The characteristics function of Poisson distribution is $\phi_X(t)=e^{\lambda(e^{it}-1)}, t \in R$.
Proof
The characteristics function of Poisson random variable $X$ is
$$ \begin{eqnarray*} \phi_X(t) &=& E(e^{itx}) \\ &=& \sum_{x=0}^\infty e^{itx} \frac{e^{-\lambda}\lambda^x}{x!}\\ &=& e^{-\lambda}\sum_{x=0}^\infty \frac{(\lambda e^{it})^x}{x!}\\ &=& e^{-\lambda}\cdot e^{\lambda e^{it}}\\ &=& e^{\lambda(e^{it}-1)}, \; t\in R. \end{eqnarray*} $$
Probability generating function of Poisson Distribution
The probability generating function of Poisson distribution is $P_X(t)=e^{\lambda(t-1)}$.
Proof
Let $X\sim P(\lambda)$ distribution. Then the m.g.f. of $X$ is
$$ \begin{eqnarray*} P_X(t) &=& E(t^x) \\ &=& \sum_{x=0}^\infty t^x \frac{e^{-\lambda}\lambda^x}{x!}\\ &=& e^{-\lambda}\sum_{x=0}^\infty \frac{(\lambda t)^x}{x!}\\ &=& e^{-\lambda}\cdot e^{\lambda t}\\ &=& e^{\lambda(t-1)}. \end{eqnarray*} $$
Additive Property of Poisson Distribution
The sum of two independent Poisson variates is also a Poisson variate.
That is, if $X_1$ and $X_2$ are two independent Poisson variate with parameters $\lambda_1$ and $\lambda_2$ respectively then $X_1+X_2 \sim P(\lambda_1+\lambda_2)$.
Proof
Let $X_1$ and $X_2$ be two independent Poisson variate with parameters $\lambda_1$ and $\lambda_2$ respectively.
Then the MGF of $X_1$ is $M_{X_1}(t) =e^{\lambda_1(e^t-1)}$ and the MGF of $X_2$ is $M_{X_2}(t) =e^{\lambda_2(e^t-1)}$.
Let $Y=X_1+X_2$. Then the MGF of $Y$ is
$$ \begin{eqnarray*} M_Y(t) &=& E(e^{tY}) \\ &=& E(e^{t(X_1+X_2)}) \\ &=& E(e^{tX_1} e^{tX_2}) \\ &=& E(e^{tX_1})\cdot E(e^{tX_2})\\ & & \quad \qquad (\because X_1, X_2 \text{ are independent })\\ &=& M_{X_1}(t)\cdot M_{X_2}(t)\\ &=& e^{\lambda_1(e^t-1)}\cdot e^{\lambda_2(e^t-1)}\\ &=& e^{(\lambda_1+\lambda_2)(e^t-1)}. \end{eqnarray*} $$
which is the m.g.f. of Poisson variate with parameter $\lambda_1+\lambda_2$.
Hence, by uniqueness theorem of MGF, $Y=X_1+X_2$ follows a Poisson distribution with parameter $\lambda_1+\lambda_2$.
Mode of Poisson distribution
The condition for mode of Poisson distribution is $\lambda-1 \leq x\leq \lambda$.
Proof
The mode is that value of $x$ for which $P(x)$ is greater that or equal to $P(x-1)$ and $P(x+1)$, i.e., $P(x-1)\leq P(x) \geq P(x+1)$.
Now, $P(x-1)\leq P(x)$ gives
$$ \begin{eqnarray*} \frac{e^{-\lambda}\lambda^{(x-1)}}{(x-1)!} &\leq& \frac{e^{-\lambda}\lambda^{x}}{x!} \\ x &\leq & \lambda. \end{eqnarray*} $$
And, $P(x) \geq P(x+1)$ gives
$$ \begin{eqnarray*} \frac{e^{-\lambda}\lambda^{x}}{x!} &\leq& \frac{e^{-\lambda}\lambda^{(x+1)}}{(x+1)!} \\ \lambda-1 &\leq & x. \end{eqnarray*} $$
Hence, the condition for mode of Poisson distribution is
$$ \begin{equation*} \lambda-1 \leq x\leq \lambda. \end{equation*} $$
Recurrence relation for raw moments
The recurrence relation for raw moments of Poisson distribution is
$$ \begin{equation*} \mu_{r+1}^\prime = \lambda \bigg[ \frac{d\mu_r^\prime}{d\lambda} + \mu_r^\prime\bigg]. \end{equation*} $$
Recurrence relation for central moments
The recurrence relation for central moments of Poisson distribution is
$$ \begin{equation*} \mu_{r+1} = \lambda \bigg[ \frac{d\mu_r}{d\lambda} + r\mu_{r-1}\bigg]. \end{equation*} $$
Recurrence relation for probabilities
The recurrence relation for probabilities of Poisson distribution is
$$ \begin{equation*} P(X=x+1) = \frac{\lambda}{x+1}\cdot P(X=x), \; x=0,1,2\cdots. \end{equation*} $$
Hope this tutorial helps you understand Poisson distribution and various results related to Poisson distributions.
