Confidence interval for difference in means when variances are unknown and equal
In this tutorial we will discuss step by step solution to some numerical problems on confidence interval for difference in means when the population variances are unknown and equal.
Example 1
A high school language course is given in two sections, each using a different teaching method.
The first section has $21$ students, and the grades in that section have a mean of $82.6$ and a standard deviation of $8.6$.
In the second section, with $43$ students, the mean of the grades is $85.2$, with a standard deviation of $7.9$.
Compute 95% confidence interval for the difference between mean grades of first section and second section. (Assume equal variances)
Solution
Let $\mu_1$ be the mean grade of first section students and $\mu_2$ be the mean grade of second section students.
Given that $n_1 = 21$, $\overline{x} =82.6$, $s_1 = 8.6$, $n_2 =43$, $\overline{y} =85.2$ and $s_2 = 7.9$.
We want to determine $95$% confidence interval estimate for the difference $(\mu_1-\mu_2)$.
Step 1 Specify the confidence level $(1-\alpha)$
Confidence level is $1-\alpha = 0.95$. Thus, the level of significance is $\alpha = 0.05$.
Step 2 Given information
Given that $n_1 = 21$, $\overline{x}= 82.6$, $s_1 = 8.6$, $n_2 = 43$, $\overline{y}= 85.2$, $s_2 = 7.9$.
Step 3 Specify the formula
$100(1-\alpha)$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is
$$ \begin{aligned} (\overline{x} -\overline{y})- E & \leq (\mu_1-\mu_2) \leq (\overline{x} -\overline{y}) + E. \end{aligned} $$
where $E = t_{\alpha/2,n_1+n_2-2}*s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}$ is the margin of error, $t_{\alpha/2, n_1+n_2-2}$ is the $t$ value providing an area of $\alpha/2$ in the upper tail of the students’ $t$ distribution with $n_1+n_2-2$ degrees of freedom and $s_p$ is the estimate of pooled standard deviation.
Step 4 Determine the critical value
The degrees of freedom is $df=n_1+n_2-2=21-43-2=62$.
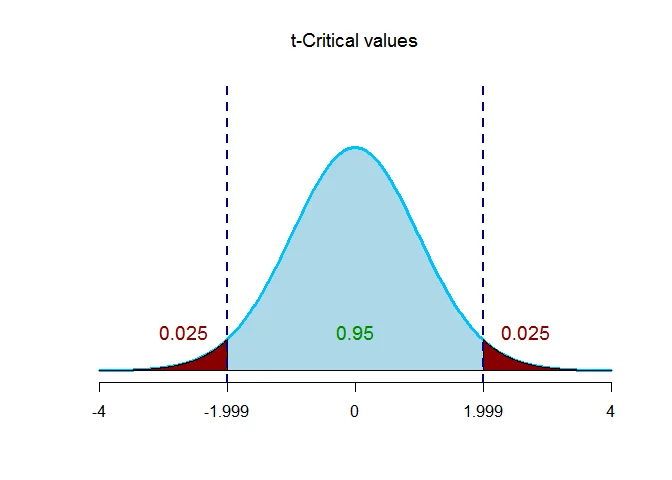
The critical value $t_{\alpha/2,n_1+n_2-2} = t_{0.025,62} = 1.999$.
Step 5 Compute the margin of error
Since the variances are equal, the estimate of pooled standard deviation is
$$ \begin{aligned} s_p & = \sqrt{\frac{(n_1-1)s_1^2 +(n_2-1)s_2^2}{n_1+n_2-2}}\\ & = \sqrt{\frac{(21-1)8.6^2 +(43-1)7.9^2}{21+43-2}}\\ & = 8.1324. \end{aligned} $$
The margin of error for difference of means $\mu_1-\mu_2$ is
$$ \begin{aligned} E & = t_{\alpha/2,n_1+n_2-2} s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}\\ & = 1.999*8.1324 \sqrt{\frac{1}{21}+\frac{1}{43}}\\ & = 4.328. \end{aligned} $$
Step 6 Determine the confidence interval
$95$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is
$$ \begin{aligned} (\overline{x} -\overline{y})- E & \leq (\mu_1-\mu_2) \leq (\overline{x} -\overline{y}) + E\\ (82.6-85.2) - 4.328 & \leq (\mu_1-\mu_2) \leq (82.6-85.2) + 4.328\\ -6.928 & \leq (\mu_1-\mu_2) \leq 1.728. \end{aligned} $$
Thus, $95$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is $(-6.928,1.728)$.
Interpretation
We can be $95$% confident that the true mean difference $(\mu_1-\mu_2)$ is between $-6.928$ and $1.728$.
Example 2
A rope company produces ropes on two production lines. The tensile strength is an important measure of quality.
A test of randomly selected ropes yields the following results:
| Summary | Rope 1 | Rope 2 |
|---|---|---|
| Mean Tensile Strength | 7087 kg | 7200 kg |
| SD | 425kg | 415kg |
| Sample size | 25 | 20 |
The company assumes the populations of rope tensile strengths are approximately normal with equal variances. Construct 90 % confidence interval for the difference between mean tensile strength for Rope 1 and Rope 2.
Solution
Let $\mu_1$ be the mean tensile strength of Rope 1 and $\mu_2$ be the mean tensile strength of Rope 2s.
Given that $n_1 = 25$, $\overline{x} =7087$, $s_1 = 425$, $n_2 =20$, $\overline{y} =7200$ and $s_2 = 415$.
We want to determine $90$% confidence interval estimate for the difference $(\mu_1-\mu_2)$.
Step 1 Specify the confidence level $(1-\alpha)$
Confidence level is $1-\alpha = 0.9$. Thus, the level of significance is $\alpha = 0.1$.
Step 2 Given information
Given that $n_1 = 25$, $\overline{x}= 7087$, $s_1 = 425$, $n_2 = 20$, $\overline{y}= 7200$, $s_2 = 415$.
Step 3 Specify the formula
$100(1-\alpha)$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is
$$ \begin{aligned} (\overline{x} -\overline{y})- E & \leq (\mu_1-\mu_2) \leq (\overline{x} -\overline{y}) + E. \end{aligned} $$
where $E = t_{\alpha/2,n_1+n_2-2}*s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}$ is the margin of error, $t_{\alpha/2, n_1+n_2-2}$ is the $t$ value providing an area of $\alpha/2$ in the upper tail of the students’ $t$ distribution with $n_1+n_2-2$ degrees of freedom and $s_p$ is the estimate of pooled standard deviation.
Step 4 Determine the critical value
The degrees of freedom is $df=n_1+n_2-2=25-20-2=43$.
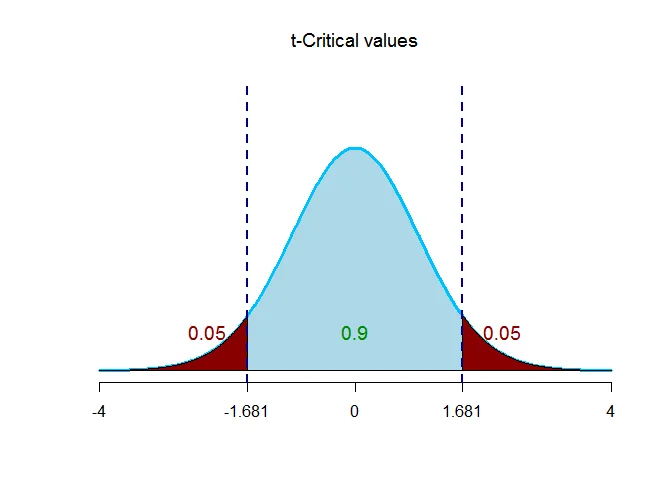
The critical value $t_{\alpha/2,n_1+n_2-2} = t_{0.05,43} = 1.681$.
Step 5 Compute the margin of error
Since the variances are equal, the estimate of pooled standard deviation is
$$ \begin{aligned} s_p & = \sqrt{\frac{(n_1-1)s_1^2 +(n_2-1)s_2^2}{n_1+n_2-2}}\\ & = \sqrt{\frac{(25-1)425^2 +(20-1)415^2}{25+20-2}}\\ & = 420.6107. \end{aligned} $$
The margin of error for difference of means $\mu_1-\mu_2$ is
$$ \begin{aligned} E & = t_{\alpha/2,n_1+n_2-2} s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}\\ & = 1.681*420.6107 \sqrt{\frac{1}{25}+\frac{1}{20}}\\ & = 212.114. \end{aligned} $$
Step 6 Determine the confidence interval
$90$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is
$$ \begin{aligned} (\overline{x} -\overline{y})- E & \leq (\mu_1-\mu_2) \leq (\overline{x} -\overline{y}) + E\\ (7087-7200) - 212.114 & \leq (\mu_1-\mu_2) \leq (7087-7200) + 212.114\\ -325.114 & \leq (\mu_1-\mu_2) \leq 99.114. \end{aligned} $$
Thus, $90$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is $(-325.114,99.114)$.
Interpretation
We can be $90$% confident that the true mean difference $(\mu_1-\mu_2)$ is between $-325.114$ and $99.114$.
