CI for difference between two population means (variances are known)
In this tutorial we will discuss some examples on confidence interval for difference in means when the population variances are known.
Example 1
Two kinds of thread are being compared for tensile strength. Fourty pieces of each type of thread are tested under similar conditions.
Brand A has an average tensile strength of 81.6 kilograms with a standard deviation of 4.5 kilograms, while brand B had an average tensile strength of 84.5 kilograms with a standard deviation of 5.1 kilograms.
Construct a 98% confidence interval for the difference of the population means.
Solution
Given that $n_1 = 40$, $\overline{x}_1 =81.6$, $\sigma_1 = 4.5$, $n_2 =40$, $\overline{x}_2 =84.5$ and $\sigma_2 = 5.1$.
We wish to determine $98$% confidence interval estimate for the difference $(\mu_1-\mu_2)$.
Step 1 Specify the confidence level $(1-\alpha)$
Confidence level is $1-\alpha = 0.98$. Thus, the level of significance is $\alpha = 0.02$.
Step 2 Given information
Given that $n_1 = 40$, $\overline{x}_1= 81.6$, $\sigma_1 = 4.5$, $n_2 = 40$, $\overline{x}_2= 84.5$, $\sigma_2 = 5.1$.
Step 3 Specify the formula
$100(1-\alpha)$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is
$$ \begin{aligned} (\overline{x}_1 -\overline{x}_2)- E & \leq (\mu_1-\mu_2) \leq (\overline{x}_1 -\overline{x}_2) + E. \end{aligned} $$
where $E = Z_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}$ and $Z_{\alpha/2}$ is the $Z$ value providing an area of $\alpha/2$ in the upper tail of the standard normal probability distribution.
Step 4 Determine the critical value
The critical value of $Z$ for given level of significance is $Z_{\alpha/2}$.
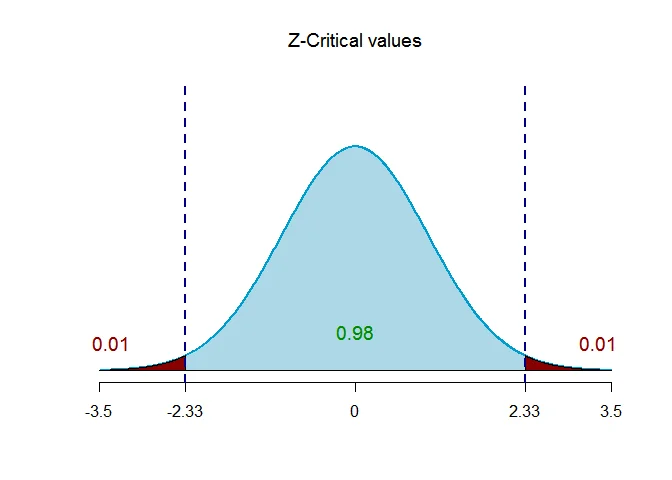
Thus $Z_{\alpha/2} = Z_{0.01} = 2.33$.
Step 5 Compute the margin of error
The margin of error for difference of means $\mu_1-\mu_2$ is
$$ \begin{aligned} E & = Z_{\alpha/2} \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\ & = 2.33 \sqrt{\frac{4.5^2}{40}+\frac{5.1^2}{40}}\\ & = 2.506. \end{aligned} $$
Step 6 Determine the confidence interval
$98$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is
$$ \begin{aligned} (\overline{x}_1 -\overline{x}_2)- E & \leq \mu_1-\mu_2 \leq (\overline{x}_1 -\overline{x}_2) + E\\ (81.6-84.5) - 2.506 & \leq \mu_1-\mu_2 \leq (81.6-84.5) + 2.506\\ -5.406 & \leq \mu_1-\mu_2 \leq -0.394. \end{aligned} $$
Thus, $98$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is $(-5.406,-0.394)$.
Interpretation
We Can be $98$% confident that the true difference in the mean tensile strength between the two brands is between $-5.4057$ and $-0.3943$.
Example 2
Two groups of students (Mathematics majors and Computer majors) are given a problem solving task on logical reasoning.
The results about the logical reasong scores are as follows:
| . | Mathematics majors | Computer majors |
|---|---|---|
| Sample size | 38 | 42 |
| Sample mean | 82.4 | 80.5 |
| Population standard deviation | 3.9 | 3.6 |
Find the 95% confidence interval of the true difference in mean lo.
Solution
Given that $n_1 = 38$, $\overline{x}_1 =82.4$, $\sigma_1 = 3.9$, $n_2 =42$, $\overline{x}_2 =80.5$ and $\sigma_2 = 3.6$.
Here we wish to determine $95$% confidence interval estimate for the difference $(\mu_1-\mu_2)$.
Step 1 Specify the confidence level $(1-\alpha)$
Confidence level is $1-\alpha = 0.95$. Thus, the level of significance is $\alpha = 0.05$.
Step 2 Given information
Given that $n_1 = 38$, $\overline{x}_1= 82.4$, $\sigma_1 = 3.9$, $n_2 = 42$, $\overline{x}_2= 80.5$, $\sigma_2 = 3.6$.
Step 3 Specify the formula
$100(1-\alpha)$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is
$$ \begin{aligned} (\overline{x}_1 -\overline{x}_2)- E & \leq (\mu_1-\mu_2) \leq (\overline{x}_2 -\overline{x}_2) + E. \end{aligned} $$
where $E = Z_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}$ and $Z_{\alpha/2}$ is the $Z$ value providing an area of $\alpha/2$ in the upper tail of the standard normal probability distribution.
Step 4 Determine the critical value
The critical value of $Z$ for given level of significance is $Z_{\alpha/2}$.
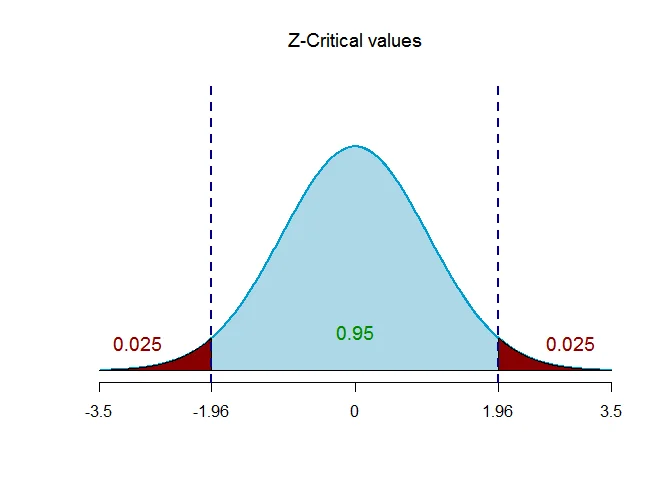
Thus $Z_{\alpha/2} = Z_{0.025} = 1.96$.
Step 5 Compute the margin of error
The margin of error for difference of means $\mu_1-\mu_2$ is
$$ \begin{aligned} E & = Z_{\alpha/2} \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\ & = 1.96 \sqrt{\frac{3.9^2}{38}+\frac{3.6^2}{42}}\\ & = 1.65. \end{aligned} $$
Step 6 Determine the confidence interval
$95$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is
$$ \begin{aligned} (\overline{x}_1 -\overline{x}_2)- E & \leq \mu_1-\mu_2 \leq (\overline{x}_1 -\overline{x}_2) + E\\ (82.4-80.5) - 1.65 & \leq \mu_1-\mu_2 \leq (82.4-80.5) + 1.65\\ 0.25 & \leq \mu_1-\mu_2 \leq 3.55. \end{aligned} $$
Thus, $95$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is $(0.25,3.55)$.
Interpretation
We can be $95$% confident that the true difference in logical reasoning task by mathematics majors and computer majors is between $0.25$ and $3.55$.
