CI for difference between two population means with unknown and unequal variances
In this tutorial we will discuss step by step solution to some numerical problems on confidence interval for difference in means when the population variances are unknown and unequal.
Example 1
To compare the mean lifespans of African elephants in the wild and in a zoo, you randomly select several lifespans from both locations.
The results are given below:
| Summary | Wild | Zoo |
|---|---|---|
| Sample mean | 56.0 year | 16.9 year |
| Sample SD | 8.6 year | 3.8 year |
| Sample size | 20 | 12 |
Construct a 95% confidence interval for the difference in mean lifespans of elephants in the wild and in a zoo.
Solution
Let $\mu_1$ be the mean lifespan of elephants in wilde location and $\mu_2$ be the mean lifespan of elephants in zoo.
Assume that the population variances are unequal.
Given that $n_1 = 20$, $\overline{x} =56$, $s_1 = 8.6$, $n_2 =12$, $\overline{y} =16.9$ and $s_2 = 3.8$.
We want to determine $95$% confidence interval estimate for the difference $(\mu_1-\mu_2)$.
Step 1 Specify the confidence level $(1-\alpha)$
Confidence level is $1-\alpha = 0.95$. Thus, the level of significance is $\alpha = 0.05$.
Step 2 Given information
Given that $n_1 = 20$, $\overline{x}= 56$, $s_1 = 8.6$, $n_2 = 12$, $\overline{y}= 16.9$, $s_2 = 3.8$.
Step 3 Specify the formula
$100(1-\alpha)$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is
$$ \begin{aligned} (\overline{x} -\overline{y})- E & \leq (\mu_1-\mu_2) \leq (\overline{x} -\overline{y}) + E. \end{aligned} $$
where $E = t_{\alpha/2,\nu}\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}$ and $t_{\alpha/2, \nu}$ is the $t$ value providing an area of $\alpha/2$ in the upper tail of the students’ $t$ distribution with $\nu$ degrees of freedom.
Step 4 Determine the critical value
The degrees of freedom $\nu$ can be calculated as
$$ \begin{aligned} \nu &= \frac{\bigg(\dfrac{s_1^2}{n_1}+\dfrac{s_2^2}{n_2}\bigg)^2}{\dfrac{1}{(n_1-1)}\bigg(\dfrac{s_1^2}{n_1}\bigg)^2+\dfrac{1}{(n_2-1)}\bigg(\dfrac{s_2^2}{n_2}\bigg)^2}\\ &=\frac{\bigg(\dfrac{8.6^2}{20}+\dfrac{3.8^2}{12}\bigg)^2}{\dfrac{1}{(20-1)}\bigg(\dfrac{8.6^2}{20}\bigg)^2+\dfrac{1}{(12-1)}\bigg(\dfrac{3.8^2}{12}\bigg)^2}\\ &=28 \end{aligned} $$
rounded to nearest integer.
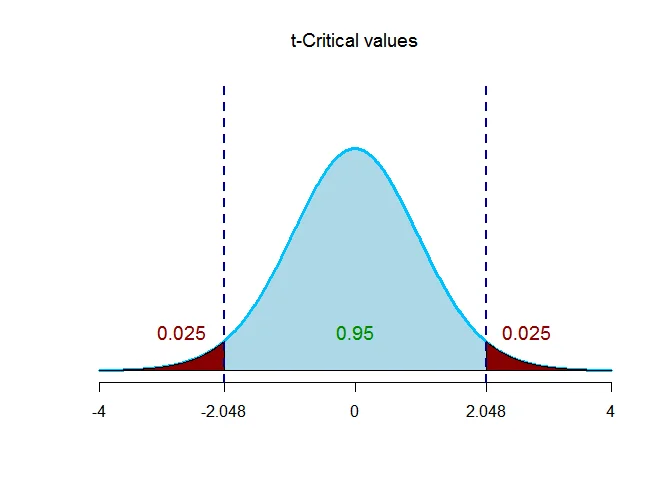
The critical value $t_{\alpha/2,\nu} = t_{0.025,28} = 2.048$.
Step 5 Compute the margin of error
The margin of error for difference of means $\mu_1-\mu_2$ is
$$ \begin{aligned} E & = t_{\alpha/2,\nu} \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}\\ & = 2.048 \sqrt{\frac{8.6^2}{20}+\frac{3.8^2}{12}}\\ & = 4.534. \end{aligned} $$
Step 6 Determine the confidence interval
$95$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is
$$ \begin{aligned} (\overline{x} -\overline{y})- E & \leq (\mu_1-\mu_2) \leq (\overline{x} -\overline{y}) + E\\ (56-16.9) - 4.534 & \leq (\mu_1-\mu_2) \leq (56-16.9) + 4.534\\ 34.566 & \leq (\mu_1-\mu_2) \leq 43.634. \end{aligned} $$
Thus, $95$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is $(34.566,43.634)$.
Interpretation
We can be $95$% confident that the true mean difference $(\mu_1-\mu_2)$ is between $34.566$ and $43.634$.
Example 2
Two methods were used to measure the brightness of independent clay samples.
The following table display the summary statistics for the two independent samples. We are interested in the difference between the two population means for the two methods.
Assume that brightness measurements are normally distributed. Also assume that the population variances are unequal.
Method A : $\overline{x}= 91.6$, $s_1 = 2.3$ and $n_1 = 12$
Method B : $\overline{y}= 92.5$, $s_2 = 1.6$ and $n_2 = 12$
Construct 90% confidence interval for the difference in mean brightness of clay.
Solution
Let $\mu_1$ be the mean brightness of the clay using Method A and $\mu_2$ be the mean brightness of the clay using Method B.
Assume that the population variances are unequal.
Given that $n_1 = 12$, $\overline{x} =91.6$, $s_1 = 2.3$, $n_2 =12$, $\overline{y} =92.5$ and $s_2 = 1.6$.
We want to determine $90$% confidence interval estimate for the difference $(\mu_1-\mu_2)$.
Step 1 Specify the confidence level $(1-\alpha)$
Confidence level is $1-\alpha = 0.9$. Thus, the level of significance is $\alpha = 0.1$.
Step 2 Given information
Given that $n_1 = 12$, $\overline{x}= 91.6$, $s_1 = 2.3$, $n_2 = 12$, $\overline{y}= 92.5$, $s_2 = 1.6$.
Step 3 Specify the formula
$100(1-\alpha)$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is
$$ \begin{aligned} (\overline{x} -\overline{y})- E & \leq (\mu_1-\mu_2) \leq (\overline{x} -\overline{y}) + E. \end{aligned} $$
where $E = t_{\alpha/2,\nu}\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}$ and $t_{\alpha/2, \nu}$ is the $t$ value providing an area of $\alpha/2$ in the upper tail of the students’ $t$ distribution with $\nu$ degrees of freedom.
Step 4 Determine the critical value
The degrees of freedom $\nu$ can be calculated as
$$ \begin{aligned} \nu &= \frac{\bigg(\dfrac{s_1^2}{n_1}+\dfrac{s_2^2}{n_2}\bigg)^2}{\dfrac{1}{(n_1-1)}\bigg(\dfrac{s_1^2}{n_1}\bigg)^2+\dfrac{1}{(n_2-1)}\bigg(\dfrac{s_2^2}{n_2}\bigg)^2}\\ &=\frac{\bigg(\dfrac{2.3^2}{12}+\dfrac{1.6^2}{12}\bigg)^2}{\dfrac{1}{(12-1)}\bigg(\dfrac{2.3^2}{12}\bigg)^2+\dfrac{1}{(12-1)}\bigg(\dfrac{1.6^2}{12}\bigg)^2}\\ &=19 \end{aligned} $$
rounded to nearest integer.
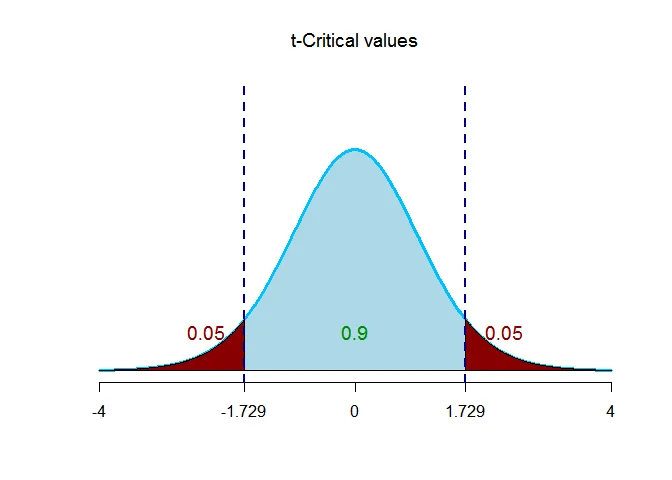
The critical value $t_{\alpha/2,\nu} = t_{0.05,19} = 1.729$.
Step 5 Compute the margin of error
The margin of error for difference of means $\mu_1-\mu_2$ is
$$ \begin{aligned} E & = t_{\alpha/2,\nu} \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}\\ & = 1.729 \sqrt{\frac{2.3^2}{12}+\frac{1.6^2}{12}}\\ & = 1.398. \end{aligned} $$
Step 6 Determine the confidence interval
$90$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is
$$ \begin{aligned} (\overline{x} -\overline{y})- E & \leq (\mu_1-\mu_2) \leq (\overline{x} -\overline{y}) + E\\ (91.6-92.5) - 1.398 & \leq (\mu_1-\mu_2) \leq (91.6-92.5) + 1.398\\ -2.298 & \leq (\mu_1-\mu_2) \leq 0.498. \end{aligned} $$
Thus, $90$% confidence interval estimate for the difference $(\mu_1-\mu_2)$ is $(-2.298,0.498)$.
Interpretation
We can be $90$% confident that the true mean difference $(\mu_1-\mu_2)$ is between $-2.298$ and $0.498$.
