Confidence Interval for ratio of variances
In this tutorial we will discuss some examples on confidence interval for ratio of variances.
Example 1
The same capacity of hard drive is manufactured on two different machines, Machine A and Machine B. Samples are taken from both machines and sample mean manufacturing times and sample variances are recorded as follows:
Machine A: $n_1=13$, $\overline{x}= 127.4$, $s_1^2= 384.16$
Machine B: $n_2=9$, $\overline{y}= 108.3$, $s_2^2 =106.09$
Compute 95% confidence interval for the ratio of variance $\sigma^2_1/\sigma^2_2$.
Solution
Let $X$ denote the manufacturing time for hard drive by machine A and let $Y$ denote the manufacturing time for hard drive by machine B. Given data is as follows:
| Summary | Machine A | Machine B |
|---|---|---|
| Sample size | $n_1= 13$ | $n_2=10$ |
| Sample variance | $s_1^2 = 384.16$ | $s_2^2 = 106.09$ |
Step 1 Specify the confidence level $(1-\alpha)$
Confidence level $=1-\alpha = 0.95$. Thus $\alpha = 0.05$.
Step 2 Given information
Specify the given information, sample sizes $n_1=13$, $n_2=10$, sample standard deviations $s_1^2=384.16$ and $s_2^2=106.09$.
Step 3 Specify the formula
$100(1-\alpha)$% confidence interval for the ratio of variances $\sigma^2_1/\sigma^2_2$ is
$$ \begin{equation*} \frac{s_1^2}{s_2^2}\cdot\frac{1}{F_{(\alpha/2, n_1-1, n_2-1)}} \leq \frac{\sigma^2_1}{\sigma^2_2} \leq \frac{s_1^2}{s_2^2}\cdot\frac{1}{F_{(1-\alpha/2, n_1-1, n_2-1)}}. \end{equation*} $$
Step 4 Determine the critical value
The critical values are $F_{(\alpha/2, n_1-1, n_2-1)}$ and $F_{(1-\alpha/2, n_1-1, n_2-1)}$.
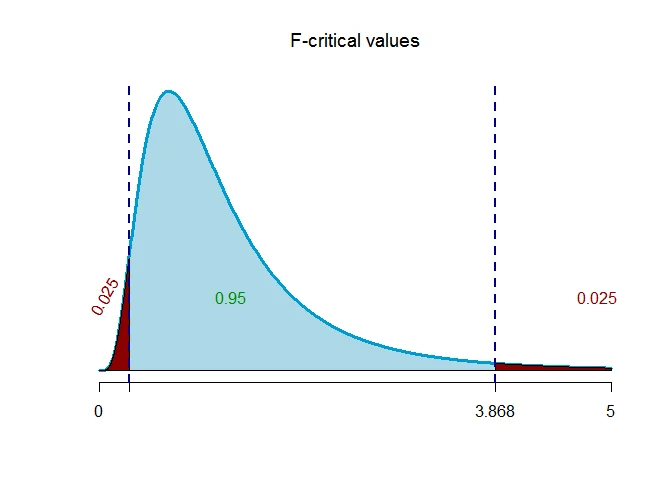
The critical values are $F_{(\alpha/2, n_1-1, n_2-1)}=F_{(0.025, 12,9)}=3.868$ and $F_{(1-\alpha/2, n_1-1, n_2-1)}=F_{(0.975, 12,9)}=0.291$.
Step 5 Determine the confidence interval
$95$% confidence interval estimate for the ratio of variances is
$$ \begin{eqnarray*} \frac{s_1^2}{s_2^2}\cdot\frac{1}{F_{(\alpha/2, n_1-1, n_2-1)}} & \leq & \frac{\sigma^2_1}{\sigma^2_2} \leq \frac{s_1^2}{s_2^2}\cdot\frac{1}{F_{(1-\alpha/2, n_1-1, n_2-1)}}\\ \frac{384.16}{106.09}\cdot\frac{1}{3.868} & \leq & \frac{\sigma^2_1}{\sigma^2_2} \leq \frac{384.16}{106.09}\cdot\frac{1}{0.291}\\ 0.9362& \leq & \frac{\sigma_1^2}{\sigma^2_2} \leq 12.4436. \end{eqnarray*} $$
Interpretation
We can be $95$% confident that the ratio of variance $\sigma^2_1/\sigma^2_2$ is between $0.9362$ and $12.4436$.
Example 2
Two different brands of batteries are tested and the variations of their voltage outputs are noted. The results are given as follows:
Brand A: $n_1=10$, $\overline{x}= 9.31$, $s_1=0.37$
Brand B: $n_2=8$, $\overline{y}= 8.82$, $s=0.31$
Construct 90% confidence interval for $\sigma^2_1/\sigma^2_2$.
Solution
Let $X$ denote the voltage output of batteries manufactred by Brand A and $Y$ denote the voltage output of batteries manufactured by brand B. Given data is as follows:
| Summary | Machine A | Machine B |
|---|---|---|
| Sample size | $n_1= 10$ | $n_2=8$ |
| Sample sd | $s_1 = 0.37$ | $s_2 = 0.31$ |
Step 1 Specify the confidence level $(1-\alpha)$
Confidence level $=1-\alpha = 0.9$. Thus $\alpha = 0.1$.
Step 2 Given information
Given that samples sizes are $n_1=10$ and $n_2=8$. The sample standard deviations are $s_1=0.37$ and $s_2=0.31$.
Step 3 Specify the formula
$100(1-\alpha)$% confidence interval for the ratio of variances $\sigma^2_1/\sigma^2_2$ is
$$ \begin{equation*} \frac{s_1^2}{s_2^2}\cdot\frac{1}{F_{(\alpha/2, n_1-1, n_2-1)}} \leq \frac{\sigma^2_1}{\sigma^2_2} \leq \frac{s_1^2}{s_2^2}\cdot\frac{1}{F_{(1-\alpha/2, n_1-1, n_2-1)}}. \end{equation*} $$
Step 4 Determine the critical value
The critical values are $F_{(\alpha/2, n_1-1, n_2-1)}$ and $F_{(1-\alpha/2, n_1-1, n_2-1)}$.

The critical values are $F_{(\alpha/2, n_1-1, n_2-1)}=F_{(0.05, 9,7)}=3.677$ and $F_{(1-\alpha/2, n_1-1, n_2-1)}=F_{(0.95, 9,7)}=0.304$.
Step 5 Determine the confidence interval
$90$% confidence interval estimate for the ratio of variances is
$$ \begin{eqnarray*} \frac{s_1^2}{s_2^2}\cdot\frac{1}{F_{(\alpha/2, n_1-1, n_2-1)}} & \leq & \frac{\sigma^2_1}{\sigma^2_2} \leq \frac{s_1^2}{s_2^2}\cdot\frac{1}{F_{(1-\alpha/2, n_1-1, n_2-1)}}\\ \frac{0.37^2}{0.31^2}\cdot\frac{1}{3.677} & \leq & \frac{\sigma^2_1}{\sigma^2_2} \leq \frac{0.37^2}{0.31^2}\cdot\frac{1}{0.304}\\ \frac{0.1369}{0.0961}\cdot\frac{1}{3.677} & \leq & \frac{\sigma^2_1}{\sigma^2_2} \leq \frac{0.1369}{0.0961}\cdot\frac{1}{0.304}\\ 0.3874& \leq & \frac{\sigma_1^2}{\sigma^2_2} \leq 4.686. \end{eqnarray*} $$
Interpretation
We can be $90$% confident that the ratio of variance $\sigma^2_1/\sigma^2_2$ is between $0.3874$ and $4.686$.
