Normal Distribution
A continuous random variable $X$ is said to have a normal
distribution if its probability density function is given by
$$ \begin{equation*} f(x;\mu, \sigma^2) = \left\{ \begin{array}{ll} \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2\sigma^2}(x-\mu)^2}, & \hbox{$-\infty< x<\infty$, $-\infty<\mu<\infty$, $\sigma^2>0$;} \\ 0, & \hbox{Otherwise.} \end{array} \right. \end{equation*} $$
where $\mu$ and $\sigma^2$ are the parameters of normal
distribution. In notation it can be written as $X\sim N(\mu,\sigma^2)$.
Mean Normal distribution
The mean of $N(\mu,\sigma^2)$ distribution is $E(X)=\mu$.
Variance of Normal distribution
Variance of $N(\mu,\sigma^2)$ distribution is $V(X)=\sigma^2$.
Example 1
A survey was conducted to measure the height of men. In the survey, respondents were grouped by age. In the 20-29 age group, the height were normally distributed, with a mean of 69.8 inches and a standard deviation of 2.1 inches. A study participant is randomly selected.
a. Find the probability that his height is less than 66.5 inches.
b. Find the probability that his height is between 65.5 and 71.6 inches.
c. Find the probability that his height is more than 72.3 inches.
Solution
Let $X$ denote the height of randomly selected participant. Given that $X\sim N(69.8, 2.1^2)$.
That is $\mu = 69.8$ and $\sigma = 2.1$.
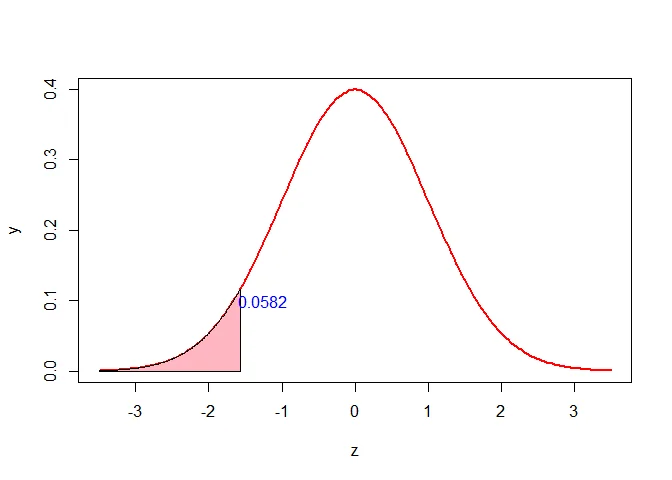
a. The probability that the study participant selected at random is less than 66.5 inches tall is $P(X<66.5)$.
The $Z$ score that corresponds to $66.5$ is
$$ \begin{aligned} z&=\dfrac{X-\mu}{\sigma}\\ &=\dfrac{66.5-69.8}{2.1}\\ &\approx-1.57 \end{aligned} $$
The probability that the study participant selected at random is less than 66.5 inches tall is
$$ \begin{aligned} P(X< 66.5) &=P(Z< -1.57)\\ &=0.0582 \end{aligned} $$
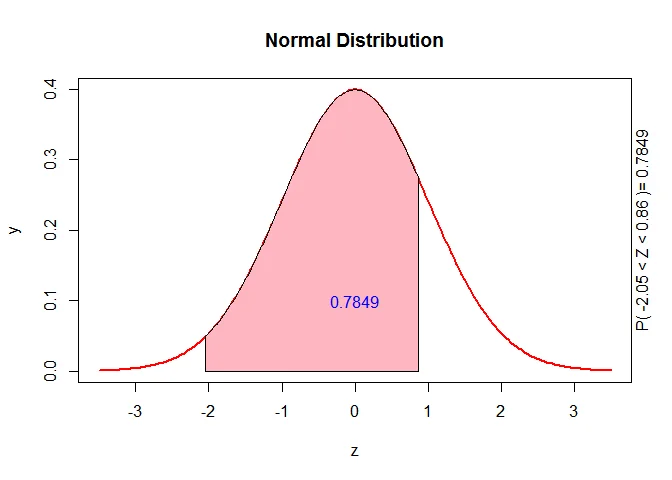
b. The probability that the study participant selected at random is between $65.5$ and $71.6$ inches tall is $P(65.5\leq X \leq 71.6)$.
The $Z$ score that corresponds to $65.5$ is
$$ \begin{aligned} z&=\dfrac{X-\mu}{\sigma}\\ &=\dfrac{65.5-69.8}{2.1}\\ &\approx-2.05 \end{aligned} $$
and the $Z$ score that corresponds to $71.6$ is
$$ \begin{aligned} z&=\dfrac{X-\mu}{\sigma}\\ &=\dfrac{71.6-69.8}{2.1}\\ &\approx0.86 \end{aligned} $$
Thus the probability that the study participant selected at random is between $65.5$ and $71.6$ inches tall is
$$ \begin{aligned} P(65.5 \leq X\leq 71.6) &=P(-2.05 \leq Z\leq 0.86)\\ &= P(Z<0.86) -P(Z< -2.05)\\ &=0.8051-0.0202\\ &= 0.7849 \end{aligned} $$
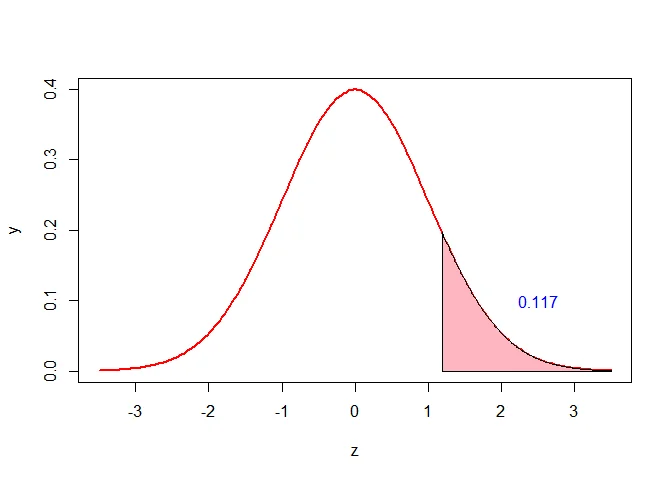
c. The probability that the study participant selected at random is more than 72.3 inches tall is $P(X>72.3)$.
The $Z$ score that corresponds to $72.3$ is
$$ \begin{aligned} z&=\dfrac{X-\mu}{\sigma}\\ &=\dfrac{72.3-69.8}{2.1}\\ &\approx1.19 \end{aligned} $$
The probability that the study participant selected at random is more than 72.3 inches tall is
$$ \begin{aligned} P(X> 72.3) &=1-P(X<72.3)\\ &=1-P(Z < 1.19)\\ &=1-0.883\\ &=0.117 \end{aligned} $$
Example 2
The grade point averages of a large number of college students are approximately normally distributed with a mean of 2.4 and a standard deviation of 0.8.
a. What percentage of students will possess a grade point average in excess of 3.0?
b. What percentage of students will possess a grade point average less than 2.2?
c. What percentage of students will possess a grade point average between 2.1 and 2.8?
Solution
Let $X$ denote the grade point average of college students. Given that $X\sim N(2.4, 0.8^2)$.
That is $\mu = 2.4$ and $\sigma = 0.8$.
a. The probability that the students will possess a grade point average in excess of $3$ is $P(X>3)$.
The $Z$ score that corresponds to $3$ is
$$ \begin{aligned} z&=\dfrac{X-\mu}{\sigma}\\ &=\dfrac{3-2.4}{0.8}\\ &\approx0.75 \end{aligned} $$
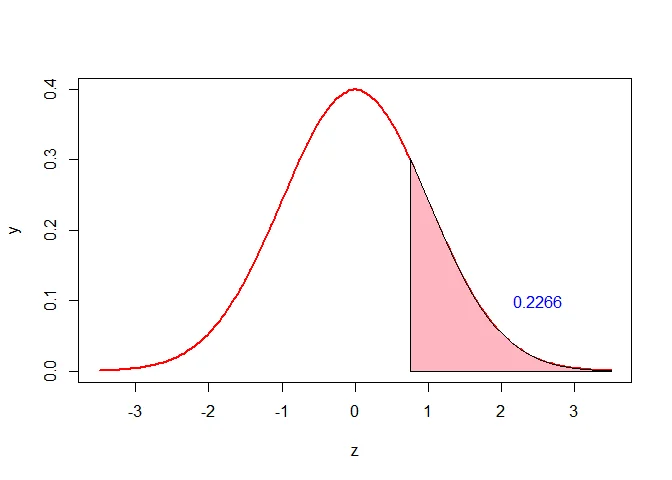
The probability that the students will possess a grade point average in excess of $3$ is
$$ \begin{aligned} P(X> 3) &=1-P(X<3)\\ &=1-P(Z < 0.75)\\ &=1-0.7734\\ &=0.2266 \end{aligned} $$
b. The probability that students will possess a grade point average less than $2.2$ is $P(X<2.2)$.
The $Z$ score that corresponds to $2.2$ is
$$ \begin{aligned} z&=\dfrac{X-\mu}{\sigma}\\ &=\dfrac{2.2-2.4}{0.8}\\ &\approx-0.25 \end{aligned} $$
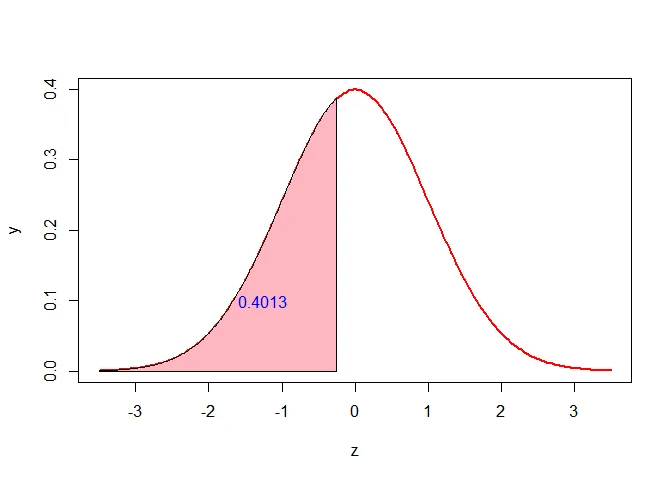
The probability that students will possess a grade point average less than $2.2$ is
$$ \begin{aligned} P(X< 2.2) &=P(Z< -0.25)\\ &=0.4013 \end{aligned} $$
c. The probability that students will possess a grade point average between $2.1$ and $2.8$ is $P(2.1\leq X \leq 2.8)$.
The $Z$ score that corresponds to $2.1$ is
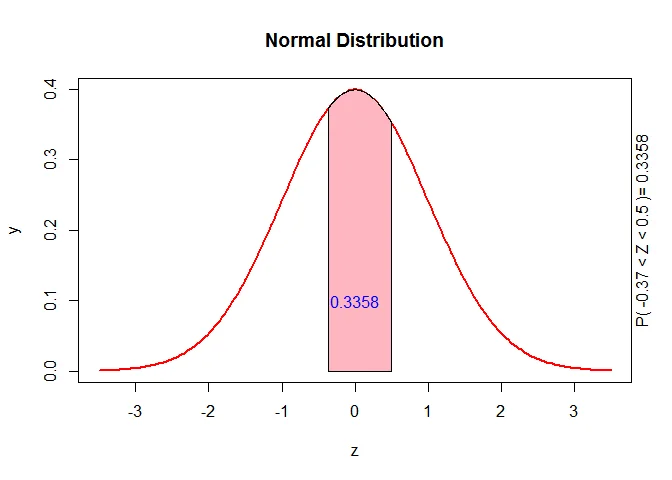
$$ \begin{aligned} z&=\dfrac{X-\mu}{\sigma}\\ &=\dfrac{2.1-2.4}{0.8}\\ &\approx-0.37 \end{aligned} $$
and the $Z$ score that corresponds to $2.8$ is
$$ \begin{aligned} z&=\dfrac{X-\mu}{\sigma}\\ &=\dfrac{2.8-2.4}{0.8}\\ &\approx0.5 \end{aligned} $$
The probability that students will possess a grade point average between $2.1$ and $2.8$ is
$$ \begin{aligned} P(2.1 \leq X\leq 2.8) &=P(-0.37 \leq Z\leq 0.5)\\ &= P(Z<0.5) -P(Z< -0.37)\\ &=0.6915-0.3557\\ &= 0.3358 \end{aligned} $$