Normal Distribution
Normal distribution is one of the most fundamental distribution in Statistics. It is also known as Gaussian distribution.
Definition
A continuous random variable $X$ is said to have a normal
distribution with parameters $\mu$ and $\sigma^2$ if its probability density function is given by
$$ \begin{equation*} f(x;\mu, \sigma^2) = \left\{ \begin{array}{ll} \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2\sigma^2}(x-\mu)^2}, & \hbox{$-\infty< x<\infty$,} \\ & \hbox{$-\infty<\mu<\infty$, $\sigma^2>0$;} \\ 0, & \hbox{Otherwise.} \end{array} \right. \end{equation*} $$
where $e= 2.71828…$ and $\pi = 3.1425926…$.
The parameter $\mu$ is called the location parameter (as it changes the location of density curve) and $\sigma^2$ is called the scale parameter of normal distribution (as it changes the scale of density curve).
In notation it can be written as $X\sim N(\mu,\sigma^2)$.
Graph of normal distribution
Following is the graph of probability density function of normal distribution. Here the means are different ($\mu = 0, 1,2$) while standard deviations are same ($\sigma=1$).
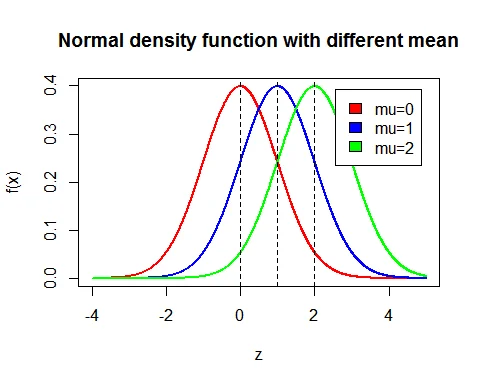
Graph of normal distribution
Following is the graph of probability density function of normal distribution. Here the means are same ($\mu = 0$) while standard deviations are different ($\sigma=1, 2, 3$).
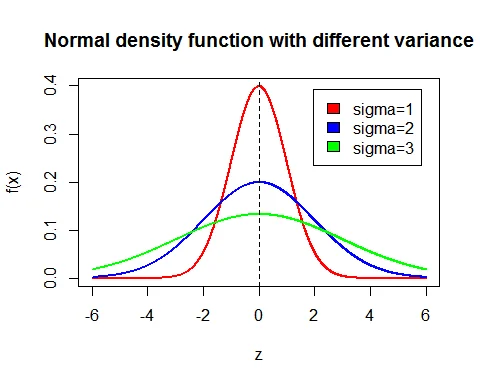
Mean Normal distribution
The mean of $N(\mu,\sigma^2)$ distribution is $E(X)=\mu$.
Proof
$$ \begin{eqnarray*} \text{Mean } &=& E(X) \\ &=& \int_{-\infty}^\infty x f(x)\; dx\\ &=& \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^\infty xe^{-\frac{1}{2\sigma^2}(x-\mu)^2} \; dx. \end{eqnarray*} $$
Let $\dfrac{x-\mu}{\sigma}=z$ $\Rightarrow x=\mu+\sigma z$.
Therefore, $dx = \sigma dz$. And if $x = \pm \infty$, $z=\pm \infty$. Hence,
$$ \begin{eqnarray*} \text{Mean } &=& \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^\infty (\mu+\sigma z)e^{-\frac{1}{2}z^2}\sigma \;dz\\ &=& \frac{\mu }{\sqrt{2\pi}}\int_{-\infty}^\infty e^{-\frac{1}{2}z^2}\; dz+\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty ze^{-\frac{1}{2}z^2} \;dz\\ & & \qquad (\text{ Second integrand is an odd function of $Z$})\\ &=& \frac{\mu }{\sqrt{2\pi}}\int_{-\infty}^\infty e^{-\frac{1}{2}z^2}\; dz+\frac{1}{\sqrt{2\pi}}\times 0\\ &=& \frac{\mu }{\sqrt{2\pi}}\sqrt{2\pi}\quad (\because \int_{-\infty}^\infty e^{-\frac{1}{2}z^2}\; dz = \sqrt{2\pi})\\ &=& \mu. \end{eqnarray*} $$
Variance of Normal distribution
Variance of $N(\mu,\sigma^2)$ distribution is $V(X)=\sigma^2$.
Proof
$$ \begin{eqnarray*} \text{Variance } &=& E(X-\mu)^2 \\ &=& \int_{-\infty}^\infty (x-\mu)^2 f(x)\; dx\\ &=& \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^\infty (x-\mu)^2e^{-\frac{1}{2\sigma^2}(x-\mu)^2} \; dx. \end{eqnarray*} $$
Let $\dfrac{x-\mu}{\sigma}=z$ $\Rightarrow x=\mu+\sigma z$.
Therefore, $dx = \sigma dz$. And if $x = \pm \infty$, $z=\pm \infty$. Hence,
$$ \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \text{Variance } &=& \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^\infty \sigma^2 z^2e^{-\frac{1}{2}z^2}\sigma \;dz\\ &=& \frac{2\sigma^2}{\sqrt{2\pi}}\int_{0}^\infty z^2e^{-\frac{1}{2}z^2}\; dz\\ & & \qquad (\text{Integrand is an even function of $Z$}) \end{eqnarray*} $$
Let $z^2=y$, $z=\sqrt{y}$ $\Rightarrow dz = \frac{dy}{2\sqrt{y}}$ and
$z=0 \Rightarrow y=0$, $z=\infty\Rightarrow y=\infty$. Hence,
$$ \begin{eqnarray*} \text{Variance } &=& \frac{2\sigma^2}{\sqrt{2\pi}}\int_{0}^\infty ye^{-\frac{1}{2}y}\; \frac{dy}{2\sqrt{y}}\\ &=& \frac{\sigma^2}{\sqrt{2\pi}}\int_{0}^\infty y^{\frac{1}{2}}e^{-\frac{1}{2}y}\; dy\\ &=& \frac{\sigma^2}{\sqrt{2\pi}}\int_{0}^\infty y^{\frac{3}{2}-1}e^{-\frac{1}{2}y}\; dy\\ &=&\frac{\sigma^2}{\sqrt{2\pi}}\frac{\Gamma(\frac{3}{2})}{(\frac{1}{2})^{\frac{3}{2}}}\\ &=&\frac{\sigma^2}{\sqrt{2\pi}}\frac{\frac{1}{2}\Gamma(\frac{1}{2})}{(\frac{1}{2})^{\frac{3}{2}}}\\ &=&\frac{\sigma^2\sqrt{\pi}}{\sqrt{\pi}}=\sigma^2. \end{eqnarray*} $$
Hence, variance of normal distribution is $\sigma^2$.
Central Moments of Normal Distribution
All the odd order central moment of $N(\mu,\sigma^2)$ distribution are $0$.
Proof
$$ \begin{eqnarray*} \mu_{2r+1} &=& E(X-\mu)^{2r+1} \\ &=& \int_{-\infty}^\infty (x-\mu)^{2r+1} f(x)\; dx\\ &=& \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^\infty (x-\mu)^{2r+1}e^{-\frac{1}{2\sigma^2}(x-\mu)^2} \; dx. \end{eqnarray*} $$
Let $\dfrac{x-\mu}{\sigma}=z$ $\Rightarrow x=\mu+\sigma z$.
Therefore, $dx = \sigma dz$. And if $x = \pm \infty$, $z=\pm \infty$. Hence,
$$ \begin{eqnarray*} \mu_{2r+1} &=& \frac{\sigma^{2r+1}}{\sigma\sqrt{2\pi}}\int_{-\infty}^\infty z^{2r+1}e^{-\frac{1}{2}z^2}\sigma \;dz\\ &=& 0 \qquad (\because \text{Integrand is an odd function of $Z$}). \end{eqnarray*} $$
Hence, all the odd order central moments of normal distribution are zero, i.e., $\mu_1=\mu_3=\mu_5= \cdots = 0$.
Even order central moments of $N(\mu,\sigma^2)$ distribution
The $(2r)^{th}$ order central moment of $N(\mu,\sigma^2)$ distribution is
$$ \begin{equation*} \mu_{2r}= \frac{\sigma^{2r}(2r)!}{2^r (r)!}. \end{equation*} $$
Proof
$$ \begin{eqnarray*} \mu_{2r} &=& E(X-\mu)^{2r} \\ &=& \int_{-\infty}^\infty (x-\mu)^{2r} f(x)\; dx\\ &=& \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^\infty (x-\mu)^{2r}e^{-\frac{1}{2\sigma^2}(x-\mu)^2} \; dx. \end{eqnarray*} $$
Let $\dfrac{x-\mu}{\sigma}=z$ $\Rightarrow x=\mu+\sigma z$.
Therefore, $dx = \sigma dz$. And if $x = \pm \infty$, $z=\pm \infty$. Hence,
$$ \begin{eqnarray*} \mu_{2r} &=& \frac{\sigma^{2r}}{\sigma\sqrt{2\pi}}\int_{-\infty}^\infty z^{2r}e^{-\frac{1}{2}z^2}\sigma \;dz\\ &=& 2 \frac{\sigma^{2r}}{\sigma\sqrt{2\pi}}\int_{0}^\infty z^{2r}e^{-\frac{1}{2}z^2}\sigma \;dz\\ & & \qquad (\because \text{Integrand is an even function of $Z$}). \end{eqnarray*} $$
Let $z^2=y$, $z=\sqrt{y}$ $\Rightarrow dz = \frac{dy}{2\sqrt{y}}$ and $z=0 \Rightarrow y=0$, $z=\infty\Rightarrow y=\infty$. Hence,
$$ \begin{eqnarray*} \mu_{2r} &=& \frac{2\sigma^{2r}}{\sqrt{2\pi}}\int_{0}^\infty y^re^{-\frac{1}{2}y}\; \frac{dy}{2\sqrt{y}}\\ &=& \frac{\sigma^{2r}}{\sqrt{2\pi}}\int_{0}^\infty y^{r-\frac{1}{2}}e^{-\frac{1}{2}y}\; dy\\ &=& \frac{\sigma^{2r}}{\sqrt{2\pi}}\int_{0}^\infty y^{r+\frac{1}{2}-1}e^{-\frac{1}{2}y}\; dy\\ &=&\frac{\sigma^{2r}}{\sqrt{2\pi}}\frac{\Gamma(r+\frac{1}{2})}{(\frac{1}{2})^{r+\frac{1}{2}}}\\ &=&\frac{\sigma^{2r}}{\sqrt{2\pi}}\frac{(r-\frac{1}{2})(r-\frac{3}{2})\cdots \frac{3}{2}\frac{1}{2}\Gamma(\frac{1}{2})}{(\frac{1}{2})^{r+\frac{1}{2}}}\\ &=&\frac{\sigma^{2r}}{\sqrt{\pi}}\frac{(r-\frac{1}{2})(r-\frac{3}{2})\cdots \frac{3}{2}\frac{1}{2}\sqrt{\pi}}{(\frac{1}{2})^{r}}\\ &=&\sigma^{2r}(2r-1)(2r-3)\cdots 3\times 1\\ &=& \sigma^{2r}\frac{2r(2r-1)(2r-2)(2r-3)\cdots 3\times 2\times 1}{2r(2r-2)(2r-4)\cdots 4\times 2} \\ \mu_{2r} &=& \frac{\sigma^{2r}(2r)!}{2^r (r)!}. \end{eqnarray*} $$
Hence,
$$ \begin{equation*} \mu_2 = \sigma^2,\; \mu_4 = 3\sigma^4. \end{equation*} $$
Coefficient of Skewness
The coefficient of skewness of $N(\mu,\sigma^2)$ distribution is $0$.
Proof
$$ \begin{equation*} \beta_1 = \frac{\mu_3^2}{\mu_2^3} = \frac{0}{\sigma^6} =0. \end{equation*} $$
Hence normal distribution is symmetric.
Kurtosis of Normal distribution
The coefficient of kurtosis of $N(\mu,\sigma^2)$ distribution is $3$.
Proof
$$ \begin{equation*} \beta_2 = \frac{\mu_4}{\mu_2^2}= \frac{3\sigma^4}{\sigma^4}=3. \end{equation*} $$
Hence, normal distribution is mesokurtic.
M.G.F. of Normal Distribution
The m.g.f. of $N(\mu,\sigma^2)$ distribution is
$$ \begin{equation*} M_X(t)=e^{t\mu +\frac{1}{2}t^2\sigma^2}. \end{equation*} $$
Proof
The moment generating function of normal distribution with parameter $\mu$ and $\sigma^2$ is
$$ \begin{eqnarray*} M_X(t) &=& E(e^{tX}) \\ &=&\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^\infty e^{tx}e^{-\frac{1}{2\sigma^2}(x-\mu)^2} \; dx. \end{eqnarray*} $$
Let $\dfrac{x-\mu}{\sigma}=z$ $\Rightarrow x=\mu+\sigma z$.
Therefore, $dx = \sigma dz$. And if $x = \pm \infty$, $z=\pm \infty$. Hence,
$$ \begin{eqnarray*} M_X(t) &=& \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^\infty e^{t(\mu+\sigma z)}e^{-\frac{1}{2}z^2} \; \sigma dz\\ &=& \frac{e^{t\mu}}{\sqrt{2\pi}}\int_{-\infty}^\infty e^{t\sigma z}e^{-\frac{1}{2}z^2} \; dz\\ &=& \frac{e^{t\mu}}{\sqrt{2\pi}}\int_{-\infty}^\infty e^{-\frac{1}{2}(z^2-2t\sigma z)} \; dz\\ &=& \frac{e^{t\mu}}{\sqrt{2\pi}}\int_{-\infty}^\infty e^{-\frac{1}{2}(z^2-2t\sigma z+t^2\sigma^2-t^2\sigma^2)} \; dz\\ &=& \frac{e^{t\mu}}{\sqrt{2\pi}}\int_{-\infty}^\infty e^{-\frac{1}{2}(z-t\sigma)^2} e^{\frac{1}{2}t^2\sigma^2} \; dz\\ &=& \frac{e^{t\mu +\frac{1}{2}t^2\sigma^2}}{\sqrt{2\pi}}\int_{-\infty}^\infty e^{-\frac{1}{2}(z-t\sigma)^2} \; dz. \end{eqnarray*} $$
Let $z-t\sigma=u$ $\Rightarrow dz=du$ and $z=\pm \infty\Rightarrow u=\pm \infty$.
$$ \begin{eqnarray*} M_X(t) &=& \frac{e^{t\mu +\frac{1}{2}t^2\sigma^2}}{\sqrt{2\pi}}\int_{-\infty}^\infty e^{-\frac{1}{2}u^2} \; du.\\ &=&\frac{e^{t\mu +\frac{1}{2}t^2\sigma^2}}{\sqrt{2\pi}}\sqrt{2\pi}\\ &=&e^{t\mu +\frac{1}{2}t^2\sigma^2}. \end{eqnarray*} $$
C.G.F. of Normal Distribution
The c.g.f. of $N(\mu,\sigma^2)$ distribution is
$$ \begin{equation*} K_x(t)= \mu t + \frac{1}{2}t^2\sigma^2. \end{equation*} $$
Proof
The moment generating function of normal distribution with parameter $\mu$ and $\sigma^2$ is
$$ \begin{eqnarray*} M_X(t) &=& e^{\mu t + \frac{1}{2}t^2\sigma^2}. \end{eqnarray*} $$
Then the cumulant generating function of normal distribution is given by
$$ \begin{eqnarray*} K_x(t) &=& \log_e M_X(t) \\ &=& \mu t + \frac{1}{2}t^2\sigma^2. \end{eqnarray*} $$
Cumulants
$\kappa_1 = \mu_1^\prime =$ coefficient of $t$ in the expansion of $K_X(t)$ = $\mu$ = mean.
$\kappa_2 = \mu_2 =$ coefficient of $\dfrac{t^2}{2!}$ in the expansion of $K_X(t)$ = $\sigma^2$ = variance.
$\kappa_3 = \mu_3 =$ coefficient of $\dfrac{t^3}{3!}$ in the expansion of $K_X(t)$ = 0.
$\kappa_4 = \mu_4-3\kappa_2^2 =$ coefficient of $\dfrac{t^4}{4!}$ in the expansion of $K_X(t)$ = 0.
$\Rightarrow \mu_4 =0+3 (\sigma^2)^2 = 3\sigma^4$.
The coefficient of skewness is
$$ \begin{equation*} \beta_1 = \frac{\mu_3^2}{\mu_2^3} = 0. \end{equation*} $$
Hence normal distribution is symmetric.
The coefficient of kurtosis is
$$ \begin{equation*} \beta_2 = \frac{\mu_4}{\mu_2^2}= \frac{3\sigma^4}{\sigma^4}=3. \end{equation*} $$
Hence, normal distribution is mesokurtic.
Characteristics function of normal distribution
The characteristics function of $N(\mu,\sigma^2)$ distribution is
$$ \begin{equation*} \phi_X(t)=e^{it\mu -\frac{1}{2}t^2\sigma^2}. \end{equation*} $$
Proof
The characteristics function of normal distribution with parameter $\mu$ and $\sigma^2$ is
$$ \begin{eqnarray*} \phi_X(t) &=& E(e^{itX}) \\ &=& M_X(it)\\ &=&e^{it\mu +\frac{1}{2}(it)^2\sigma^2}\\ &=&e^{it\mu -\frac{1}{2}t^2\sigma^2}\\ & & \qquad (\because i^2 = -1). \end{eqnarray*} $$
(replacing $t$ by $it$ in moment generating function of $X$).
Median of Normal Distribution
The median of $N(\mu,\sigma^2)$ distribution is $M =\mu$.
Proof
Let $M$ be the median of the distribution. Hence
$$ \begin{eqnarray*} \int_{-\infty}^M f(x) \; dx = \frac{1}{2} & & \\ \text{i.e., } \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^M e^{-\frac{1}{2\sigma^2}(x-\mu)^2} \; dx & = & \frac{1}{2}. \end{eqnarray*} $$
Let $\dfrac{x-\mu}{\sigma}=z$ $\Rightarrow x=\mu+\sigma z$.
Therefore, $dx = \sigma dz$. Also, for $x = -\infty$, $z=- \infty$ and for $x=M$, $z= \frac{M-\mu}{\sigma}$. Hence,
$$ \begin{eqnarray*} \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\frac{M-\mu}{\sigma}} e^{-\frac{1}{2}z^2} \; dz & = & \frac{1}{2}\\ \int_{-\infty}^{\frac{M-\mu}{\sigma}} e^{-\frac{1}{2}z^2} \; dz & = & \sqrt{\frac{\pi}{2}} \end{eqnarray*} $$
We know that
$$ \begin{eqnarray*} \int_{-\infty}^{\infty} e^{-\frac{1}{2}z^2} \; dz & = & \sqrt{2\pi}\\\nonumber 2\int_{-\infty}^{0} e^{-\frac{1}{2}z^2} \; dz & = & \sqrt{2\pi}\\ \int_{-\infty}^{0} e^{-\frac{1}{2}z^2} \; dz & = & \sqrt{\frac{\pi}{2}}. \end{eqnarray*} $$
Comparing the two integrals, we get
$$ \begin{equation*} \frac{M-\mu}{\sigma}=0 \Rightarrow M=\mu. \end{equation*} $$
Hence,the median of the normal distribution is $M=\mu$.
Mode of Normal Distribution
The mode of $N(\mu,\sigma^2)$ distribution is $\mu$.
Proof
The p.d.f. of normal distribution is
$$ \begin{equation*} f(x;\mu, \sigma^2) = \left\{ \begin{array}{ll} \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2\sigma^2}(x-\mu)^2}, & \hbox{$-\infty< x<\infty$, $-\infty<\mu<\infty$, $\sigma^2>0$;} \\ 0, & \hbox{Otherwise.} \end{array} \right. \end{equation*} $$
Taking $\log_e$ of $f(x)$, we get
$$ \begin{equation*} \log_e f(x) = c-\frac{1}{2\sigma^2}(x-\mu)^2 \end{equation*} $$
Differentiating w.r.t. $x$ and equating to zero, we get
$$ \begin{eqnarray*} & & \frac{\partial \log_e f(x)}{\partial x}=0\\ \Rightarrow & &0-\frac{2}{2\sigma^2}(x-\mu)=0\\ \Rightarrow & &x=\mu. \end{eqnarray*} $$
And $\frac{\partial^2 \log_e f(x)}{\partial x^2}\bigg|_{x=\mu} <0$.
Hence by the principle maxima and minima, at $x=\mu$, the density
function becomes maximum.
Therefore, mode of normal distribution is $\mu$.
For normal distribution, mean = median = mode = $\mu$. Hence normal distribution is symmetrical distribution and it is symmetric about $x=\mu$.
Mean deviation about mean
The mean deviation about mean is
$$ \begin{equation*} E[|X-\mu|]=\sqrt{\frac{2}{\pi}}\sigma. \end{equation*} $$
Proof
$$ \begin{eqnarray*} E(|X-\mu|) &=& \int_{-\infty}^\infty |x-\mu| f(x)\; dx\\ &=& \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^\infty |x-\mu|e^{-\frac{1}{2\sigma^2}(x-\mu)^2} \; dx. \end{eqnarray*} $$
Let $\dfrac{x-\mu}{\sigma}=z$ $\Rightarrow x=\mu+\sigma z$.
Therefore, $dx = \sigma dz$. And if $x = \pm \infty$, $z=\pm \infty$. Hence,
$$ \begin{eqnarray*} E(|X-\mu|)&=& \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^\infty |\sigma z|e^{-\frac{1}{2}z^2}\sigma \;dz\\ &=& \frac{\sigma}{\sqrt{2\pi}}\int_{-\infty}^\infty |z|e^{-\frac{1}{2}z^2}\; dz\\ &=& \frac{2\sigma }{\sqrt{2\pi}}\int_{0}^\infty ze^{-\frac{1}{2}z^2}\; dz\\ &=& \frac{\sqrt{2}\sigma}{\sqrt{\pi}}\int_{0}^\infty ze^{-\frac{1}{2}z^2}\; dz \end{eqnarray*} $$
Let $z^2=y$, $z=\sqrt{y}$ $\Rightarrow dz = \frac{dy}{2\sqrt{y}}$ and $z=0 \Rightarrow y=0$, $z=\infty\Rightarrow y=\infty$. Hence,
$$ \begin{eqnarray*} E(|X-\mu|) &=& \frac{\sqrt{2}\sigma}{\sqrt{\pi}}\int_{0}^\infty \sqrt{y}e^{-\frac{1}{2}y}\; \frac{dy}{2\sqrt{y}}\\ &=& \frac{\sqrt{2}\sigma}{2\sqrt{\pi}}\int_{0}^\infty e^{-\frac{1}{2}y}\; dy\\ &=& \frac{\sqrt{2}\sigma}{2\sqrt{\pi}}\int_{0}^\infty y^{1-1}e^{-\frac{1}{2}y}\; dy\\ &=&\frac{\sqrt{2}\sigma}{2\sqrt{\pi}}\frac{\Gamma(1)}{(\frac{1}{2})^1}\\ &=&\sqrt{\frac{2}{\pi}}\sigma. \end{eqnarray*} $$
Hence, for normal distribution, mean deviation about mean in $\sqrt{\frac{2}{\pi}}\sigma$.
The sum of two independent normal variates is also a normal variate.
Let $X$ and $Y$ are independent normal variates with $N(\mu_1, \sigma^2_1)$ and $N(\mu_2, \sigma^2_2)$ distribution respectively. Then $X+Y\sim N(\mu_1+\mu_2,\sigma^2_1+\sigma^2_2)$.
Proof
Let $X \sim N(\mu_1, \sigma^2_1)$ and $Y\sim N(\mu_2, \sigma^2_2)$.
Moreover, $X$ and $Y$ are independently distributed. The m.g.f. of $X$ is
$$ \begin{equation*} M_X(t) = e^{t\mu_1 +\frac{1}{2} t^2\sigma^2_1} \end{equation*} $$
and
$$ \begin{equation*} M_Y(t) = e^{t\mu_2 +\frac{1}{2} t^2\sigma^2_2} \end{equation*} $$
Let, $Z = X+Y$. Then the m.g.f. of $Z$ is
$$ \begin{eqnarray*} M_Z(t) &= & E(e^{tZ})\\ &=& E(e^{t(X+Y)})\\ &=& E(e^{tX}\cdot e^{tY})\\ &=& E(e^{tX})\cdot E(e^{tY}),\;\qquad (X \text{ and } Y \text{ are independent}\\ &=& M_X(t)\cdot M_Y(t) \\ &=& e^{t\mu_1 +\frac{1}{2} t^2\sigma^2_1}\cdot e^{t\mu_2 +\frac{1}{2} t^2\sigma^2_2}\\ &=&e^{t(\mu_1+\mu_2) +\frac{1}{2} t^2(\sigma^2_1+\sigma^2_2)}, \end{eqnarray*} $$
which is the m.g.f. of normal variate with parameters $\mu_1+\mu_2$ and $\sigma^2_1+\sigma^2_2$.
Hence, $X+Y \sim N(\mu_1+\mu_2,\sigma^2_1+\sigma^2_2)$.
The difference of two independent normal variates is also a normal variate.
Let $X$ and $Y$ are independent normal variates with $N(\mu_1, \sigma^2_1)$ and $N(\mu_2, \sigma^2_2)$ distribution respectively. Then $X-Y\sim N(\mu_1-\mu_2,\sigma^2_1+\sigma^2_2)$.
Proof
Let $X \sim N(\mu_1, \sigma^2_1)$ and $Y\sim N(\mu_2, \sigma^2_2)$.
Moreover, $X$ and $Y$ are independently distributed. The m.g.f. of $X$ is
$$ \begin{equation*} M_X(t) = e^{t\mu_1 +\frac{1}{2} t^2\sigma^2_1} \end{equation*} $$
and
$$ \begin{equation*} M_Y(t) = e^{t\mu_2 +\frac{1}{2} t^2\sigma^2_2} \end{equation*} $$
Let, $Z = X-Y$. Then the m.g.f. of $Z$ is
$$ \begin{eqnarray*} M_Z(t) &= & E(e^{tZ})\\ &=& E(e^{t(X-Y)})\\ &=& E(e^{tX}\cdot e^{-tY})\\ &=& E(e^{tX})\cdot E(e^{-tY}),\;\qquad (X \text{ and } Y \text{ are independent)}\\ &=& M_X(t)\cdot M_Y(-t) \\ &=& e^{t\mu_1 +\frac{1}{2} t^2\sigma^2_1}\cdot e^{-t\mu_2 +\frac{1}{2}(-t)^2\sigma^2_2}\\ &=&e^{t(\mu_1-\mu_2) +\frac{1}{2} t^2(\sigma^2_1+\sigma^2_2)}, \end{eqnarray*} $$
which is the m.g.f. of normal variate with parameters $\mu_1-\mu_2$ and $\sigma^2_1+\sigma^2_2$. Hence, $X-Y \sim N(\mu_1-\mu_2,\sigma^2_1+\sigma^2_2)$.
Distribution of sample mean
Let $X_i, i=1,2,\cdots, n$ be independent sample observation from $N(\mu, \sigma^2)$ distribution then the sample mean $\overline{X}$ is normally distributed with mean $\mu$ and variance $\dfrac{\sigma^2}{n}$.
Proof
As $X_i\sim N(\mu, \sigma^2), i=1,2,\cdots, n$,
$$ \begin{equation*} M_{X_i}(t) =e^{t\mu +\frac{1}{2} t^2\sigma^2}, \; i=1,2,\cdots,n. \end{equation*} $$
Now, the m.g.f. of $\overline{X}$ is,
$$ \begin{eqnarray*} M_{\overline{X}}(t) &= & E(e^{t\overline{X}})\\ &=& E(e^{t\frac{1}{n}\sum_i X_i})\\ &=& E( e^{\frac{t}{n}X_1} e^{\frac{t}{n}X_2}\cdots e^{\frac{t}{n}X_n})\\ &=& E( e^{\frac{t}{n}X_1})\cdot E(e^{\frac{t}{n}X_2})\cdots E(e^{\frac{t}{n}X_n}),\qquad (X \text{ and } Y \text{ are independent})\\ &=& M_{X_1}(t/n)\cdot M_{X_2}(t/n)\cdots M_{X_n}(t/n) \\ &=& \prod_{i=1}^n M_{X_i}(t/n)\\ &=& \prod_{i=1}^n e^{\frac{t}{n}\mu +\frac{1}{2} \frac{t^2}{n^2}\sigma^2}\\ &=& e^{n\frac{t}{n}\mu +\frac{n}{2}\frac{t^2}{n^2}\sigma^2}\\ &=& e^{t\mu +\frac{1}{2}t^2\frac{\sigma^2}{n}}. \end{eqnarray*} $$
which is the m.g.f. of normal variate with parameters $\mu$ and $\frac{\sigma^2}{n}$. Hence, $\overline{X}\sim N(\mu,\frac{\sigma^2}{n})$.
Standard Normal Distribution
If $X\sim N(\mu, \sigma^2)$ distribution, then the variate $Z =\frac{X-\mu}{\sigma}$ is called a standard normal variate and $Z\sim N(0,1)$ distribution. The p.d.f. of standard normal variate $Z$ is
$$ \begin{equation*} f(z)= \left\{ \begin{array}{ll} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}z^2}, & \hbox{$-\infty < z<\infty$;} \\ 0, & \hbox{Otherwise.} \end{array} \right. \end{equation*} $$
Statement of the Empirical Rule
Suppose you have a normal distribution with mean $\mu$ and standard deviation $\sigma$. Then, each of the following is true:
1.68% of the data will occur within one standard deviation of the mean.
2.95% of the data will occur within two standard deviations of the mean.
3.99.7% of the data will occur within three standard deviations of the mean.
