Paired $t$-test (Dependent Sample)
In this tutorial we will discuss some numerical examples on paired t test.
Example 1
A new prep class was designed to improve AP statistics test scores. Five students were selected at random. The numbers of correct answers on two practice exams were recorded; one before the class and one after. The data recorded in the table below. We want to test if the numbers of correct answers, on average, are higher after the class.
| Student | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Before Class | 12 | 15 | 9 | 12 | 12 |
| After Class | 14 | 18 | 11 | 10 | 12 |
Is there evidence to suggest that the mean number of correct answers after the class exceeds the mean number of correct answers before the class? Use $\alpha = 0.1$.
Solution
Let $x$ denote the number of correct answer before the class and $y$ denote the number of correct answer after the class.
Because the two samples are dependent, we use paired $t$-test for testing the hypothesis problem.
The sample size $n = 5$. Let $d=x-y$.
| $x$ | $y$ | $d$ | $d-\overline{d}$ | $(d-\overline{d})^2$ | |
|---|---|---|---|---|---|
| 12 | 14 | -2 | -1 | 1 | |
| 15 | 18 | -3 | -2 | 4 | |
| 9 | 11 | -2 | -1 | 1 | |
| 12 | 10 | 2 | 3 | 9 | |
| 12 | 12 | 0 | 1 | 1 | |
| Total | -5 | 16 |
The sample mean of the difference is
$$ \begin{aligned} \overline{d}&= \frac{1}{n}\sum_{i=1}^n d_i\\ &=\frac{-5}{5}\\ &=-1 \end{aligned} $$
and the sample standard deviation of the difference is
$$ \begin{aligned} s_d&= \sqrt{\frac{1}{n-1}\sum_{i=1}^n (d_i-\overline{d})^2}\\ &=\sqrt{\frac{16}{4}}\\ &=2 \end{aligned} $$
Step 1 Hypothesis
The hypothesis testing problem is $H_0 : \mu_d = 0$ against $H_1 : \mu_d < 0$ ($\textit{left-tailed}$)
Step 2 Test Statistic
The test statistic for testing $H_0$ against $H_1$ is $$ \begin{aligned} t=\frac{\overline{d} -\mu_d}{s_d/\sqrt{n}} \end{aligned} $$
Step 3 Level of Significance
The significance level is $\alpha = 0.1$.
Step 4 Critical Value(s)
As the alternative hypothesis is $\textit{left-tailed}$, the critical value of $t$ for $4$ degrees of freedom and $\alpha = 0.1$ level of significance $\text{is}$ $\text{-1.533}$.
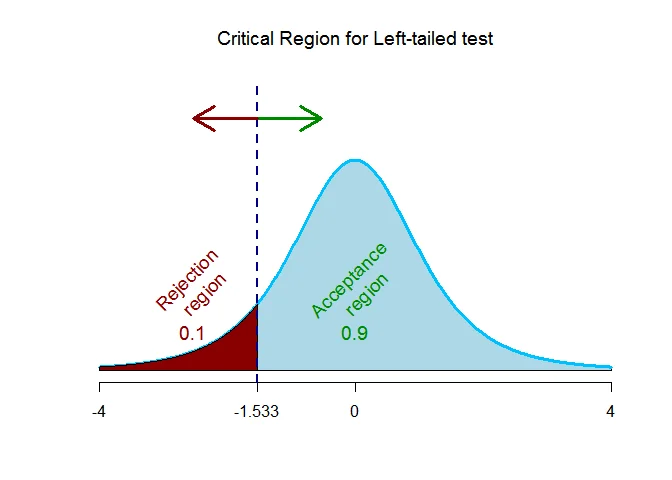
The rejection region (i.e. critical region) is $\text{t < -1.533}$.
Step 5 Computation
The test statistic for testing above hypothesis testing problem under the null hypothesis is
$$ \begin{aligned} t&=\frac{\overline{d} -\mu_d}{s_d/\sqrt{n}}\\ &= \frac{-1-0}{2/\sqrt{5}}\\ &= -1.118 \end{aligned} $$
Step 6 Decision (Traditional approach)
The test statistic is $t =-1.118$ which falls $\textit{outside}$ the critical region, we $\textit{fail to reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value approach)
The test is $\textit{left-tailed}$ test, so p-value is the area to the $\textit{left}$ of the test statistic ($t=-1.118$). That is p-value = $P(t\leq -1.118 ) = 0.1631$.
The p-value is $0.1631$ which is $\textit{greater than}$ the significance level of $\alpha = 0.1$, we $\textit{fail to reject}$ the null hypothesis at $0.1$ level of significance.
Interpretation
There is no sufficient evidence to claim that the mean number of correct answers after the class exceeds the mean number of correct answers before the class.
Example 2
A manufacturer claims that they have designed a new keyboard that will increase the speed of a typist. A following study was done : Six students were selected at random to type a term paper on a regular keyboard and on a newly designed keyboard. Which keyboard the student types on the first was chosen at random. The following table shows the number of minutes each student took to type the term paper on each keyboard. At $\alpha =0.05$, did the newly designed keyboard reduce the number of minutes to type the paper?
| Student | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| Regular | 54 | 63 | 47 | 61 | 52 | 59 |
| Newly designed | 52 | 61 | 48 | 58 | 51 | 55 |
Solution
Let $x$ denote the number of minutes to type term paper using regular keyboard and $y$ denote the number of minutes to type term paper using newly designed keyboard.
Because the two samples are dependent, we use paired $t$-test for testing the hypothesis problem.
The sample size $n = 6$. Let $d=x-y$.
| $x$ | $y$ | $d$ | $d-\overline{d}$ | $(d-\overline{d})^2$ | |
|---|---|---|---|---|---|
| 54 | 52 | 2 | 0.167 | 0.028 | |
| 63 | 61 | 2 | 0.167 | 0.028 | |
| 47 | 48 | -1 | -2.833 | 8.028 | |
| 61 | 58 | 3 | 1.167 | 1.361 | |
| 52 | 51 | 1 | -0.833 | 0.694 | |
| 59 | 55 | 4 | 2.167 | 4.694 | |
| Total | 11 | 14.8333 |
The sample mean of the difference is
$$ \begin{aligned} \overline{d}&= \frac{1}{n}\sum_{i=1}^n d_i\\ &=\frac{11}{6}\\ &=1.8333 \end{aligned} $$
and the sample standard deviation of the difference is
$$ \begin{aligned} s_d&= \sqrt{\frac{1}{n-1}\sum_{i=1}^n (d_i-\overline{d})^2}\\ &=\sqrt{\frac{14.8333}{5}}\\ &=1.7224 \end{aligned} $$
Step 1 Hypothesis
The hypothesis testing problem is $H_0 : \mu_d = 0$ against $H_1 : \mu_d > 0$ ($\textit{right-tailed}$)
Step 2 Test Statistic
The test statistic for testing $H_0$ against $H_1$ is
$$ \begin{aligned} t=\frac{\overline{d} -\mu_d}{s_d/\sqrt{n}} \end{aligned} $$
Step 3 Level of Significance
The significance level is $\alpha = 0.05$.
Step 4 Critical Value(s)
As the alternative hypothesis is $\textit{right-tailed}$, the critical value of $t$ for $5$ degrees of freedom and $\alpha = 0.05$ level of significance $\text{is}$ $\text{2.015}$.
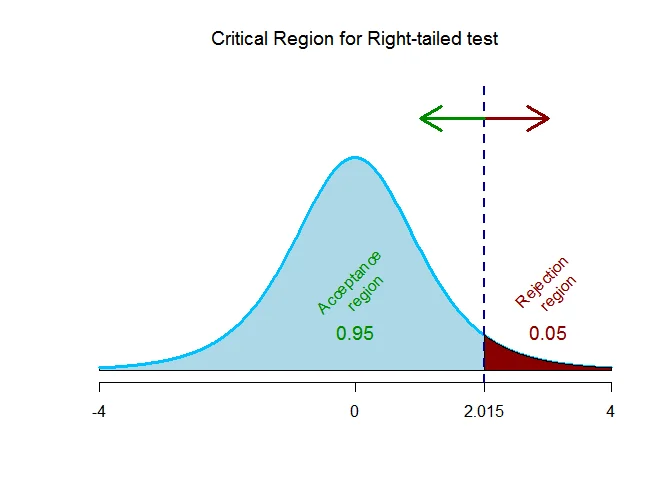
The rejection region (i.e. critical region) is $\text{t > 2.015}$.
Step 5 Computation
The test statistic for testing above hypothesis testing problem under the null hypothesis is
$$ \begin{aligned} t&=\frac{\overline{d} -\mu_d}{s_d/\sqrt{n}}\\ &= \frac{1.8333-0}{1.7224/\sqrt{6}}\\ &= 2.6072 \end{aligned} $$
Step 6 Decision (Traditional approach)
The test statistic is $t =2.6072$ which falls $\textit{inside}$ the critical region, we $\textit{reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value approach)
The test is $\textit{right-tailed}$ test, so p-value is the area to the $\textit{right}$ of the test statistic ($t=2.6072$). That is p-value = $P(t\geq 2.6072 ) = 0.0239$.
The p-value is $0.0239$ which is $\textit{less than}$ the significance level of $\alpha = 0.05$, we $\textit{reject}$ the null hypothesis at $0.05$ level of significance.
Interpretation
There is sufficient evidence to support the claim that the newly designed keyboard reduce the number of minutes to type the term paper.
Example 3
Listed below are body temperatures (in $^oF$) of subjects measured at 8:00 AM and at 12:00 AM by a physician.
Is body temperature basically the same at both times? Use $\alpha = 0.05$.
| At 8:00 AM | 97.0 | 96.2 | 97.6 | 96.4 | 97.8 | 99.2 |
|---|---|---|---|---|---|---|
| At 12:00 AM | 98.0 | 98.6 | 98.8 | 98.0 | 98.6 | 97.6 |
Solution
Let $x$ denote the body temperature (in $^oF$) of subjects at 8:00 AM and $y$ denote the body temperature (in $^oF$) of subjects at 12:00 AM.
Because the two samples are dependent, we use paired $t$-test for testing the hypothesis problem.
The sample size $n = 6$. Let $d=x-y$.
| $x$ | $y$ | $d$ | $d-\overline{d}$ | $(d-\overline{d})^2$ | |
|---|---|---|---|---|---|
| 97 | 98 | -1 | -0.1 | 0.01 | |
| 96.2 | 98.6 | -2.4 | -1.5 | 2.25 | |
| 97.6 | 98.8 | -1.2 | -0.3 | 0.09 | |
| 96.4 | 98 | -1.6 | -0.7 | 0.49 | |
| 97.8 | 98.6 | -0.8 | 0.1 | 0.01 | |
| 99.2 | 97.6 | 1.6 | 2.5 | 6.25 | |
| Total | -5.4 | 9.1 |
The sample mean of the difference is
$$ \begin{aligned} \overline{d}&= \frac{1}{n}\sum_{i=1}^n d_i\\ &=\frac{-5.4}{6}\\ &=-0.9 \end{aligned} $$
and the sample standard deviation of the difference is
$$ \begin{aligned} s_d&= \sqrt{\frac{1}{n-1}\sum_{i=1}^n (d_i-\overline{d})^2}\\ &=\sqrt{\frac{9.1}{5}}\\ &=1.3491 \end{aligned} $$
Step 1 Hypothesis
The hypothesis testing problem is $H_0 : \mu_d = 0$ against $H_1 : \mu_d \neq 0$ ($\textit{two-tailed}$)
Step 2 Test Statistic
The test statistic for testing $H_0$ against $H_1$ is
$$ \begin{aligned} t=\frac{\overline{d} -\mu_d}{s_d/\sqrt{n}} \end{aligned} $$
Step 3 Level of Significance
The significance level is $\alpha = 0.05$.
Step 4 Critical Value(s)
As the alternative hypothesis is $\textit{two-tailed}$, the critical value of $t$ for $5$ degrees of freedom and $\alpha = 0.05$ level of significance $\text{are}$ $\text{-2.571 and 2.571}$.
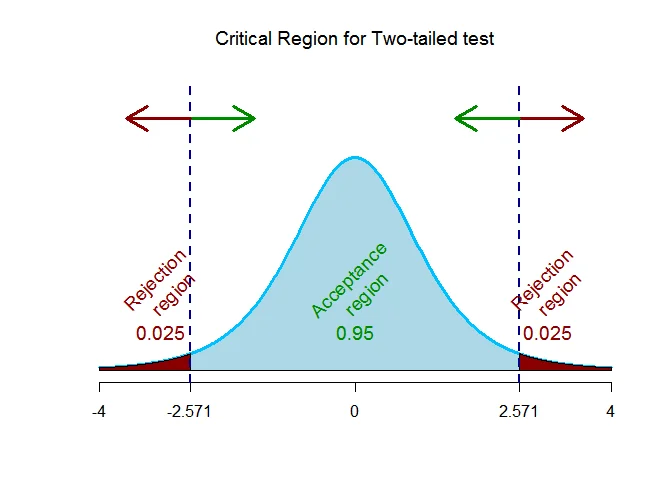
The rejection region (i.e. critical region) is $\text{t < -2.571 or t > 2.571}$.
Step 5 Computation
The test statistic for testing above hypothesis testing problem under the null hypothesis is
$$ \begin{aligned} t&=\frac{\overline{d} -\mu_d}{s_d/\sqrt{n}}\\ &= \frac{-0.9-0}{1.3491/\sqrt{6}}\\ &= -1.6341 \end{aligned} $$
Step 6 Decision (Traditional approach)
The test statistic is $t =-1.6341$ which falls $\textit{outside}$ the critical region, we $\textit{fail to reject}$ the null hypothesis.
OR
Step 6 Decison ($p$-value approach)
The test is $\textit{two-tailed}$ test, so p-value is the area to the $\textit{extreme}$ of the test statistic ($t=-1.6341$). That is p-value = $2*P(t\geq 1.6341 ) = 0.1632$.
The p-value is $0.1632$ which is $\textit{greater than}$ the significance level of $\alpha = 0.05$, we $\textit{fail to reject}$ the null hypothesis at $0.05$ level of significance.
Interpretation
We conclude that the body temperature of the subjects are same at both the times.
