Sample size to estimate mean
The minimum sample size required to estimate the population mean $\mu$ is
$$ \begin{aligned} n &= \bigg(\frac{z*\sigma}{E}\bigg)^2 \end{aligned} $$
where
- $\sigma$ is the population standard deviation
- $z=z_{\alpha/2}$ is the critical value of $Z$
- $E$ is the margin of error.
Example 1
An efficiency expert wishes to determine the average time that it takes to drill three holes in a certain metal clamp. How large a sample will she need to be 90% confident that her sample mean will be within 15 seconds of the true mean? Assume that it is known from previous studies that $\sigma = 40$ seconds.
Solution
Given that the standard deviation $\sigma =40$, margin of error $E =15$. The confidence coefficient is $1-\alpha=0.9$. Thus $\alpha = 0.1$.
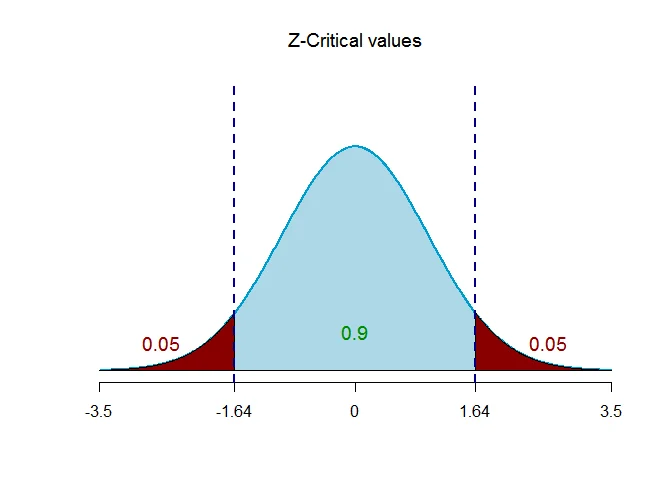
The critical value of $Z$ is $z=Z_{\alpha/2} = 1.64$.
The minimum sample size required to estimate the mean is
$$ \begin{aligned} n &= \bigg(\dfrac{z*\sigma}{E}\bigg)^2\\ & = \bigg(\dfrac{1.64*40}{15}\bigg)^2\\ & =19.126\\ &\approx 20. \end{aligned} $$
Thus, the sample of size $n=20$ will ensure that the $90$% confidence interval for the mean will have a margin of error $15$.
Example 2
An electrical firm manufactures light bulbs that have a length of life that is approximately normal with a standard deviation of 30 hours. How large a sample is needed if we wish to be 99% confident that our sample mean will be within 10 hours of the true mean?
Solution
Given that the standard deviation $\sigma =30$, margin of error $E =10$. The confidence coefficient is $1-\alpha=0.99$. Thus $\alpha = 0.01$.
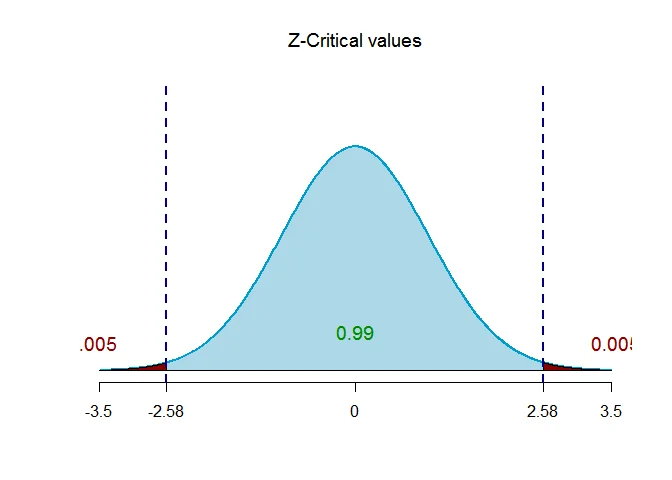
The critical value of $Z$ is $z=Z_{\alpha/2} = 2.58$.
The minimum sample size required to estimate the mean is
$$ \begin{aligned} n &= \bigg(\dfrac{z*\sigma}{E}\bigg)^2\\ & = \bigg(\dfrac{2.58*30}{10}\bigg)^2\\ & =59.9076\\ &\approx 60. \end{aligned} $$
Thus, the sample of size $n=60$ will ensure that the $99$% confidence interval for the mean will have a margin of error $10$.
Example 3
How large a sample is needed to assess the population mean, with a standard deviation of $17 with an allowable error of $1.50 at 95 percent confidence?
Solution
Given that the standard deviation $\sigma =17$, margin of error $E =1.5$. The confidence coefficient is $1-\alpha=0.95$. Thus $\alpha = 0.05$.
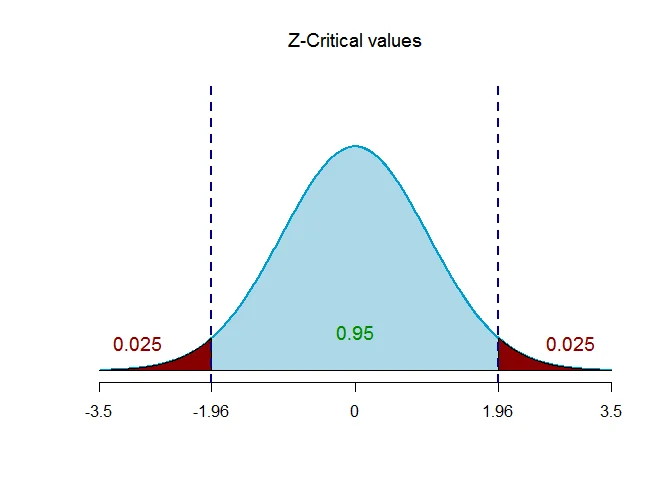
The critical value of $Z$ is $z=Z_{\alpha/2} = 1.96$.
The minimum sample size required to estimate the mean is
$$ \begin{aligned} n &= \bigg(\dfrac{z*\sigma}{E}\bigg)^2\\ & = \bigg(\dfrac{1.96*17}{1.5}\bigg)^2\\ & =493.4322\\ &\approx 494. \end{aligned} $$
Thus, the sample of size $n=494$ will ensure that the $95$% confidence interval for the mean will have a margin of error $1.5$.
