Sample size to estimate proportion
The minimum sample size required to estimate the population proportion is
$$ n =p*(1-p)\bigg(\frac{z}{E}\bigg)^2 $$
where,
-
$p$ is the proportion of success,
-
$z$ is the $Z_{\alpha/2}$ (critical value of $Z$),
-
$E$ is the margin of error.
Example 1
A survey of 1000 randomly selected registered U.S. voters found that 37% were in favor of the recent tax reform plan. A new survey is being proposed to estimate the true proportion in favor of the recent tax reform plan.
How many voters should be surveyed if the the goal is to estimate the proportion of voters within 0.05 with 90% confidence?
Solution
Given that the proportion of voters who favor the recent tax reform plan is $p =0.37$. The margin of error $E =0.05$. The confidence coefficient is $0.9$.
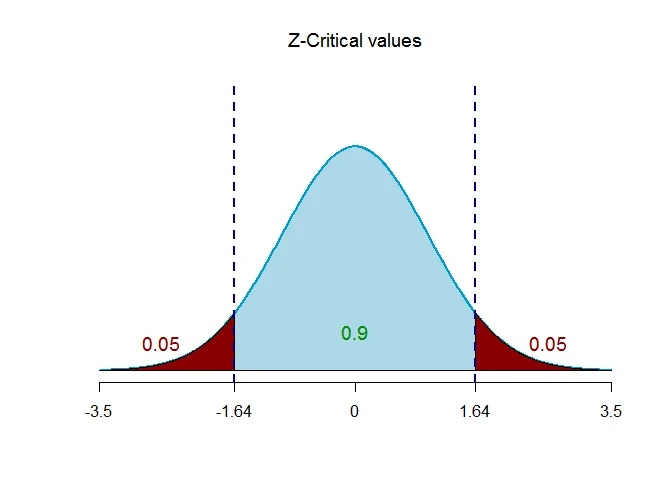
The critical value of $Z$ is $Z_{\alpha/2} = 1.64$.
The minimum sample size required to estimate the proportion voters who favor the recent tax reform plan is
$$ \begin{aligned} n&= p(1-p)\bigg(\frac{z}{E}\bigg)^2\\ &= 0.37(1-0.37)\bigg(\frac{1.64}{0.05}\bigg)^2\\ &=250.7783\\ &\approx 251. \end{aligned} $$
Thus, the sample of size $n=251$ will ensure that the $90$% confidence interval for the proportion voters who favor the recent tax reform plan will have a margin of error $0.05$.
Example 2
Suppose we know that the unemployment rate has been about 18%. However, we wish to update our estimate in order to make an important decision about the national economic policy.
Accordingly, let us say we wish to be 98% confident that the new estimate of $p$ is within 0.01 of true $p$. What is the sample size needed to achieve this?
Solution
Given that the proportion of unemployment is $p =0.18$. The margin of error $E =0.01$. The confidence coefficient is $0.98$.
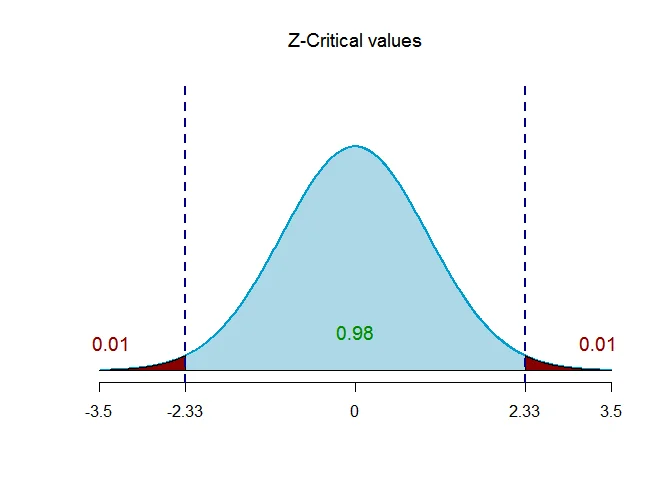
The critical value of $Z$ is $Z_{\alpha/2} = 2.33$.
The minimum sample size required to estimate the proportion of employment is
$$ \begin{aligned} n&= p(1-p)\bigg(\frac{z}{E}\bigg)^2\\ &= 0.18(1-0.18)\bigg(\frac{2.33}{0.01}\bigg)^2\\ &=8013.0564\\ &\approx 8014. \end{aligned} $$
Thus, the sample of size $n=8014$ will ensure that the $98$% confidence interval for the proportion of employment will have a margin of error $0.01$.
Example 3
An insurance company estimates 45 percent of its claims have errors. The insurance company wants to estimate with 90 percent confidence the proportion of claims with errors. What sample size is needed if they wish to be within 5 percentage points of the actual?
Solution
Given that the proportion of claims with error is $p =0.45$. The margin of error $E =0.05$. The confidence coefficient is $0.9$.
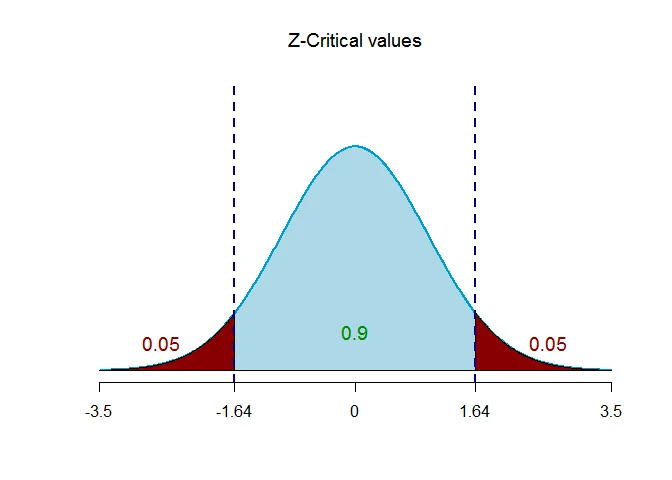
The critical value of $Z$ is $Z_{\alpha/2} = 1.64$.
The minimum sample size required to estimate the proportion of claims with error is
$$ \begin{aligned} n&= p(1-p)\bigg(\frac{z}{E}\bigg)^2\\ &= 0.45(1-0.45)\bigg(\frac{1.64}{0.05}\bigg)^2\\ &=266.2704\\ &\approx 267. \end{aligned} $$
Thus, the sample of size $n=267$ will ensure that the $90$% confidence interval for the proportion of claims with error will have a margin of error $0.05$.
