p value of the test
p-value of the test is the probability that the test statistic under null hypothesis will take on values as extreme as or more extreme than the observed value of test statistic.
The smaller p-value of the test indicate strong evidence against the null hypothesis $H_0$.
In this tutorial we discuss about how to find the $p$-value of the Z-test. The p-value of the $Z$-test depends on the direction of the alternative hypothesis.
$p$-Value of Z-test
If the test statistic $Z$ has standard normal distribution, then the $p$-value of the test for testing
a. left-tailed hypothesis is $p$-value = $P(Z\leq z_{obs})$.
b. right-tailed hypothesis is $p$-value = $P(Z\geq z_{obs})$.
c. two-tailed hypothesis is $p$-value = $2P(Z\geq |Z_{obs}|)$.
Interpretation from p-value
If the $p$-value of the test is less than or equal to the level of significance ($\alpha$) (i.e., $p \leq \alpha$), we reject the null hypothesis $H_0$ at $\alpha$ level of significance.
If the $p$-value of the test is greater than the level of significance ($\alpha$) (i.e., $p > \alpha$), we fail to reject the null hypothesis $H_0$ at $\alpha$ level of significance.
Example 1
Find the $p$-value for a right-tailed hypothesis testing problem with a test statistic $Z_{obs}=2.65$. What is your decision if the level of significance is $\alpha = 0.05$.
Solution
The test statistic is $Z_{obs}=2.65$. The alternative hypothesis is right-tailed.
Because the alternative hypothesis is right-tailed, the $p$-value of the test is given by
$$ \begin{aligned} p&=P(Z\geq Z_{obs})\\ &=P(Z\geq 2.65)\\ &= 0.004 \end{aligned} $$
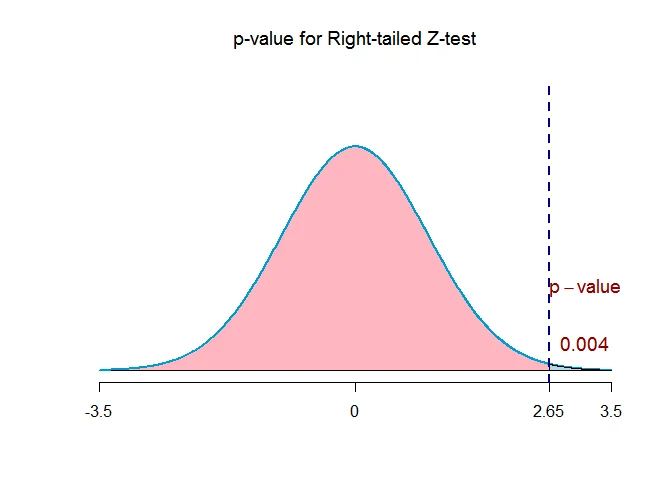
Because the p-value ($0.004$) is $\text{less than}$ the significance level $\alpha = 0.05$, we $\text{reject}$ the null hypothesis at $0.05$ level of significance.
Example 2
Find the $p$-value for a left-tailed hypothesis testing problem with a test statistic $Z_{obs}=-2.023$. What is your decision if the level of significance is $\alpha = 0.01$.
Solution
The test statistic is $Z_{obs}=-2.023$. The alternative hypothesis is left-tailed.
Because the alternative hypothesis is left-tailed, the $p$-value of the test is given by
$$ \begin{aligned} p&=P(Z\leq Z_{obs})\\ &=P(Z\leq -2.023)\\ &= 0.0215 \end{aligned} $$
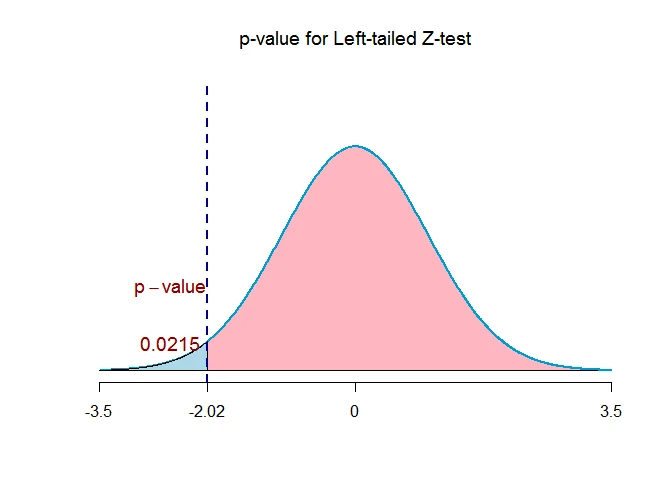
Because the p-value ($0.0215$) is $\text{greater than}$ the significance level $\alpha = 0.01$, we $\text{fail to reject}$ the null hypothesis at $0.01$ level of significance.
Example 3
Find the $p$-value for a two-tailed hypothesis testing problem with a test statistic $Z_{obs}=1.674$. What is your decision if the level of significance is $\alpha = 0.05$.
Solution
The test statistic is $Z_{obs}=1.674$. The alternative hypothesis is two-tailed.
Because the alternative hypothesis is two-tailed, the $p$-value of the test is given by
$$ \begin{aligned} p&=2*P(Z\geq |Z_{obs}|)\\ &=2*P(Z\geq |1.674|)\\ &=2*0.0471\\ &= 0.0942 \end{aligned} $$
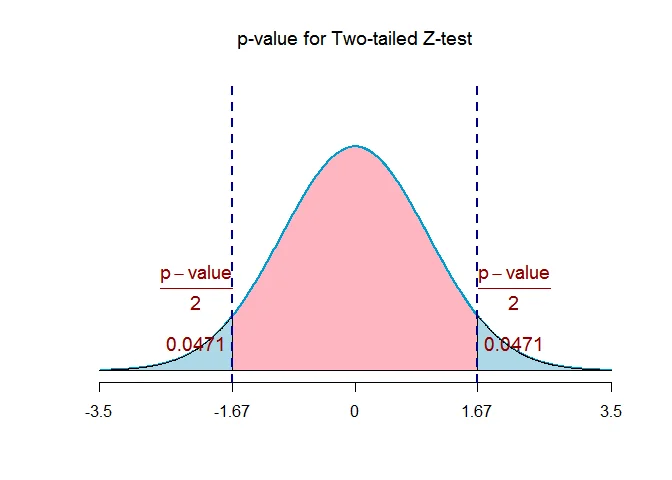
Because the p-value ($0.0942$) is $\text{greater than}$ the significance level $\alpha = 0.05$, we $\text{fail to reject}$ the null hypothesis at $0.05$ level of significance.
