Binomial Distribution Calculator
Binomial distribution calculator is used to find the probability and cumulative probabilities for binomial random variable given the number of trials ($n$) and probability of success ($p$). It also calculate mean of binomial distribution,variance of binomial distribution.
Binomial Probability Calculator
| Binomial Probability Calculator | |
|---|---|
| Number of trials ($n$): | |
| Number of success (x): | |
| Probability of success ($p$): | |
| Binomial Distribution Calculator Result | |
| Mean : $np$ | |
| Variance : $np(1-p)$ | |
| Probability : P(X = x) | |
| Cumulative Probability : P(X ≤ x) | |
| Cumulative Probability : P(X < x) | |
| Cumulative Probability : P(X ≥ x) | |
| Cumulative Probability : P(X > x) | |
How to use Binomial Distribution Calculator with step by step?
-
Enter the number of trials (n)
-
Enter the number of success (x)
-
Enter the Probability of success (p)
-
Click on Calculate button for binomial probabiity calculation
-
Calculate the mean of binomial distribution (np)
-
Calculate the variance of binomial distribution np(1-p)
-
Calculate Binomial Probability
-
Calculate binomial distribution mean
-
Calculate np(1-p) binomial distribution variance
-
Calculate cumulative probabilities
Binomial Distribution formula
The probability mass function (pmf) of Binomial distribution with parameter $n$ and $p$ is
$$ \begin{aligned} P(X=x)&=\binom{n}{x} p^x q^{n-x},\\ & \quad x=0,1,2,\cdots, n;\\ & \quad 0<p<1,q=1-p \end{aligned} $$
where
- $n =$ number of trials,
- $x =$ number of successes in $n$ trials,
- $p =$ probability of success,
- $q = 1- p =$ probability of failures.
Mean of Binomial Distribution
The mean or expected value of binomial random variable $X$ is $E(X) = np$.
Variance of Binomial distribution
The variance of Binomial random variable $X$ is $V(X) = npq$.
Below are the few numerical problems solved using binomial distribution calculator with steps by steps solution.
Binomial Distribution Calculation with Steps
Suppose that a short quiz consists of 6 multiple choice questions.Each question has four possible answers of which ony one in correct. A student guesses on every question. Find the binomial probability that a student will answer
a. five or more quetions correctly,
b. all questions correctly,
c. at most 1 questions correctly,
d. between 4 and 5 (inclusive) questions correctly.
Solution
Let $X$ be the number of questions guessed correctly out of $6$ questions.
Let $p$ be the probability of correct guess.
The binomial random variable $X$ follows a Binomial distribution with parameter $n=6$ and $p=0.25$. That is, $X\sim B(6, 0.25)$.
The probability mass function (pmf) of Binomial Distribution formula $X$ is
$$ \begin{aligned} P(X=x) &= \binom{6}{x} (0.25)^x (1-0.25)^{6-x}, \; x=0,1,\cdots, 6\\ &=\binom{6}{x} (0.25)^x (0.75)^{6-x}, \; x=0,1,\cdots,6 \end{aligned} $$
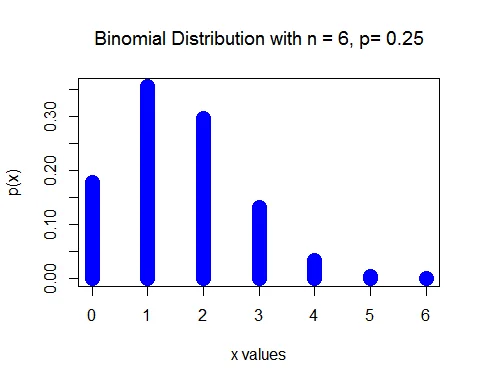
a. The probability that a student will answer $5$ or more questions correctly is
$$ \begin{aligned} P(X\geq 5) &= P(X=5)+P(X=6)\\ &= \binom{6}{5} (0.25)^{5} (0.75)^{6-5}+\binom{6}{6} (0.25)^{6} (0.75)^{6-6}\\ &= 0.0044+0.0002\\ & = 0.0046 \end{aligned} $$
b. The probability that a student will answer all questions correctly is
$$ \begin{aligned} P(X= 6) & =P(6)\\ &= \binom{6}{6} (0.25)^{6} (0.75)^{6-6}\\ & = 0.0002 \end{aligned} $$
c. The probability that a student will answer at most $1$ questions correctly is
$$ \begin{aligned} P(X\leq 1) &= P(X=0)+P(X=1)\\ &= \binom{6}{0} (0.25)^{0} (0.75)^{6-0}+\binom{6}{1} (0.25)^{1} (0.75)^{6-1}\\ &=0.178+0.356\\ &= 0.5339 \end{aligned} $$
d. The probability that a student will answer between $4$ and $5$ questions correctly is
$$ \begin{aligned} P(4\leq X\leq 5) & =P(X=4)+P(X=5)\\ &= \binom{6}{4} (0.25)^{4} (0.75)^{6-4}+\binom{6}{5} (0.25)^{5} (0.75)^{6-5}\\ & = 0.033+0.0044\\ &= 0.0374 \end{aligned} $$
Binomial Probability Calculation with steps
35% of the adults says cashews are their favorite kind of nuts. If you randomly select 10 adults and ask each adult to name his or her favorite nut, compute the binomial probability that the number of adults who say cashews are their favorite nut is
a. exactly 4,
b. less than 3,
c. at least 3,
d. at the most 2.
Solution
Let $X$ be the number of adults out of $10$ who say cashew is their favorite nut.
Let $p$ be the probability that an adults favorite nut is cashew.
Given that $p=0.35$ and $n =10$. Here $X$ follows a Binomial distribution. That is, $X\sim B(10, 0.35)$.
The probability mass function (pmf) of Binomial Distribution formula $X$ is calculated as
$$ P(X=x) = \binom{10}{x} (0.35)^x (1-0.35)^{10-x}, \; x=0,1,\cdots, 10. $$
The binomial distribution mean $X$ is
$$ \begin{aligned} \mu =E(X) &= n*p\\ &= 10*0.35\\ &= 3.5 \end{aligned} $$
and the standard deviation of binomial distribution $X$ is
$$ \begin{aligned} \sigma=\sqrt{V(X)} &=\sqrt{n*p*(1-p)}\\ &=\sqrt{10*0.35* (1- 0.35)}\\ &= 1.5083 \end{aligned} $$
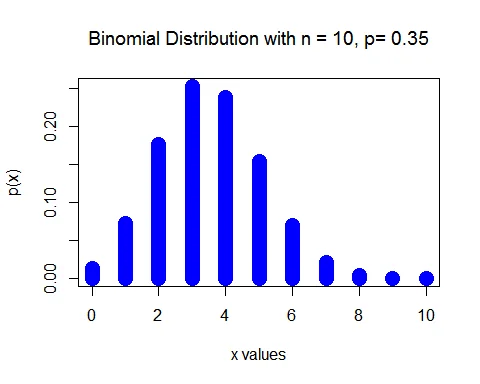
a. The probability that exactly 4 adults say cashews are their favorite nut is
$$ \begin{aligned} P(X= 4) & =P(4)\\ &= \binom{10}{4} (0.35)^{4} (1-0.35)^{10-4}\\ &= 210\times 0.015\times 0.0754\\ & = 0.2377 \end{aligned} $$
b. The probability that less than 3 adults say cashews are their favorite nut is
$$ \begin{aligned} P(X< 3) & =P(X\leq 2)\\ &= P(0)+P(1)\\ & = 0.0135+0.0725\\ & = 0.2616 \end{aligned} $$
c. The binomial probability that at least 3 adults say cashews are their favorite nut is
$$ \begin{aligned} P(X\geq 3) & =1-P(X\leq 2)\\ &= 1-(P(0)+P(1))\\ & = 1-\big(0.0135+0.0725 \big)\\ & = 0.7384 \end{aligned} $$
d. The binomial probability that at most 2 adults say cashews are their favorite nut is
$$ \begin{aligned} P(X\leq 2) & =\sum_{x=0}^{2} P(x)\\ & =P(0) + P(1) + P(2)\\ & = 0.0135+0.0725+0.1757\\ &= 0.2616 \end{aligned} $$
Binomial Probability Distribution Calculation with steps
Working Women and Computer Use : It is reported that 72% of working women use computers at work. Choose 5 working women at random. Find
a. The probability that at least 1 does not use a computer at work. b. The probability that all 5 use a computer in their jobs.
Solution
Let $X :$ the number of womens who use computer at work out of $5$.
Here $n = 5$ and $p=0.72$. The probability distribution of $X$ is Binomial distribution. That is $X\sim B(5,0.72)$.
The probability mass function (pmf) of binomial distribution formula $X$ calculated as is
$$ \begin{aligned} P(X=x) &= \binom{5}{x} (0.72)^x (1-0.72)^{5-x},\\ &\quad \; x=0,1,\cdots, 5 \end{aligned} $$
a. Probability that at least 1 doesn’t use a computer at work is same as the probability that none use computer at work.
$$ \begin{aligned} P(X= 0) & =\binom{5}{0} (0.72)^{0} (1-0.72)^{5-0}\\ & = 0.0017\\ \end{aligned} $$
b. Probability that all 5 use computer at work is
$$ \begin{aligned} P(X= 5) & =\binom{5}{5} (0.72)^{5} (1-0.72)^{5-5}\\ & = 0.1935 \end{aligned} $$
Binomial Distribution Calculation with steps
A new surgical procedure is said to be successful 75% of the time. If 4 patients undergo the surgical procedure, what is the probability that
a. all four operations are successful? b. Exactly three operations are successful? c. Less than two are successful?
Solution
Here $X$ denote the number successful operations out of 4.
Let $p$ be the probability that operation using new surgical procedure is successful.
Given that $p=0.75$ and $n =4$. Thus$X\sim B(4, 0.75)$.
The probability mass function (pmf) of binomial distribution $X$ is
$$ \begin{aligned} P(X=x) &= \binom{4}{x} (0.75)^x (1-0.75)^{4-x}, \\ &\quad \; x=0,1,\cdots, 4 \end{aligned} $$
a. The binomial probability that all four operations are successful is
$$ \begin{aligned} P(X=4) & =\binom{4}{4} (0.75)^{4} (1-0.75)^{4-4}\\ &=0.3164 \end{aligned} $$
b. The binomial probability that exactly three operations are successful is
$$ \begin{aligned} P(X=3) & =\binom{4}{3} (0.75)^{3} (1-0.75)^{4-3}\\ &=0.4219 \end{aligned} $$
c. The probability that less than two operations are successful is
$$ \begin{aligned} P(X< 2) &=P(X\leq 1)\\ &=P(X=0)+P(X=1)\\ &= 0.0039+0.0469\\ &= 0.0508 \end{aligned} $$
Cumulative Binomial Probability Calculation with steps by steps
According to a recent survey, outside of their own family members, 26% of adult Americans have no close friend to confide in. If this is the prevailing probability today, find the probability that in a random sample of n = 5 adults
a. two or more have no close friend. b. at most two have no close friend. c. Find the expected number of persons who have no close friend.
Solution
Here $X$ denote the number of adult Americans who have no close friend to confide.
$p$ be the probability that adult American who have no close friend to confide.
Given that $p=0.26$ and $n =5$. Thus$X\sim B(5, 0.26)$.
The probability mass function (pmf) of binomial distribution $X$ is
$$ \begin{aligned} P(X=x) &= \binom{5}{x} (0.26)^x (1-0.26)^{5-x},\\ &\quad\; x=0,1,\cdots, 5 \end{aligned} $$
a. The binomial probability that 2 or more have no close friend is
$$ \begin{aligned} P(X\geq 2) & =1-P(X\leq 1)\\ &= 1-\sum_{x=0}^{1} P(x)\\ & = 1-0.6117 \\ &= 1- (0.2219+0.3898)\\ & = 0.3883 \\ \end{aligned} $$
b. The probability that at most two have no close friend is
$$ \begin{aligned} P(X\leq 2) & =\sum_{x=0}^{2} P(x)\\ & =\sum_{x=0}^{2}\binom{5}{x}(0.26)^x(1-0.26)^{5-x}\\ & = 0.2219+0.3898+0.2739\\ &=0.8857. \end{aligned} $$
c. The expected number of persons who have no close friend is $n*p = 5 * 0.26 = 1.3$.
Conclusion
I hope you like above article on how to use binomial distribution calculator with steps by steps solution in solved examples.
Read more about other Statistics Calculator on below links
- Descriptive Statistics Calculators
- Hypothesis Testing Calculators
- Probability Distribution
- Confidence Interval Calculators
- Correlation Regression Calculators
- Probability Theory Calculators
- Sample Size and Power Calculators
