One sample t test calculator
The one sample t-test for mean is used to perform hypothesis testing problem for population mean when the population standard deviation is unknown. This calculator makes it easy to conduct one sample t-test for population mean.
| t-test Calculator for mean | |
|---|---|
| Population Mean ($\mu$) | |
| Sample Size ($n$) | |
| Sample Mean ($\overline{x}$) | |
| Sample Standard Deviation ($s$) | |
| Level of Significance ($\alpha$) | |
| Tail: | Left tailed Right tailed Two tailed |
| Results | |
| Standard Error of Mean: | |
| Test Statistics t: | |
| Degrees of Freedom: | |
| t-critical value: | |
| p-value: | |
How to use t test for one mean calculator?
Step 1 - Enter the Population mean
Step 2 - Enter the Sample size
Step 3 - Enter the Sample mean
Step 4 - Enter the Standard deviation
Step 5 - Enter the level of Significance ($\alpha$)
Step 6 - Select the left tailed or right tailed or two tailed for t test calculator
Step 7 - Click on “Calculate” button to calculate t test
Step 8 - Calculate Test Statistics (t)
Step 9 - Calculate Degrees of Freedom
Step 10 - Calculate t test critical value
Step 11 - Calculate p value
One sample t test
Let $X_1, X_2, \cdots, X_n$ be a random sample from a normal population with mean $\mu$ and unknown variance $\sigma^2$.
The hypothesis problem can be setup as
| Situation | Hypothesis Testing Problem |
|---|---|
| Situation A | $H_0: \mu=\mu_0$ against $H_a : \mu < \mu_0$ (Left-tailed) |
| Situation B | $H_0: \mu=\mu_0$ against $H_a : \mu > \mu_0$ (Right-tailed) |
| Situation C | $H_0: \mu=\mu_0$ against $H_a : \mu \neq \mu_0$ (Two-tailed) |
Formula
The test statistic under $H_0: \mu=\mu_0$ is
$t = \dfrac{\overline{x}-\mu_0}{SE(\overline{x})}$
where,
$\overline{x}=\dfrac{1}{n} \sum x_i$is the sample mean,$SE(\overline{x})=\dfrac{s}{\sqrt{n}}$is the standard error of mean,$s^2 =\dfrac{1}{n-1} \sum (x_i -\overline{x})^2$is the sample variance.
The test statistic t follows t distribution with $n-1$ degrees of freedom.
One Sample t test for mean
Lets understand the six steps approach used in hypothesis testing to test hypothesis about the population mean when the population standard deviation is unknown.
One sample t test for mean
Let $X_1, X_2, \cdots, X_n$ be a random sample from a normal population with mean $\mu$ and unknown variance $\sigma^2$. Let $\overline{x}=\frac{1}{n} \sum x_i$ be the sample mean and $s^2 =\frac{1}{n-1} \sum (x_i -\overline{x})^2$ be the sample variance.
Assumptions
a. The population from which, the sample drawn is assumed as Normal distribution.
b. The population variance $\sigma^2$ is unknown.
Step by Step Procedure
We wish to test the null hypothesis $H_0 : \mu = \mu_0$, where $\mu_0$ is the specified value of the population mean.
The standard error of mean is
$$ \begin{aligned} SE(\overline{x}) & = \frac{\sigma}{\sqrt{n}}=\frac{s}{\sqrt{n}} \end{aligned} $$
Step 1 State the hypothesis testing problem
The hypothesis testing problem can be structured in any one of the three situations as follows:
| Situation | Hypothesis Testing Problem |
|---|---|
| Situation A | $H_0: \mu=\mu_0$ against $H_a : \mu < \mu_0$ (Left-tailed) |
| Situation B | $H_0: \mu=\mu_0$ against $H_a : \mu > \mu_0$ (Right-tailed) |
| Situation C | $H_0: \mu=\mu_0$ against $H_a : \mu \neq \mu_0$ (Two-tailed) |
Step 2 Define the test statistic
The test statistic for testing above hypothesis is
$$ \begin{eqnarray*} t & =& \frac{\overline{x}-\mu}{SE(\overline{x})}\\ & = & \frac{\overline{x}-\mu_0}{s/\sqrt{n}} \end{eqnarray*} $$
The test statistic t follows Students’ $t$ distribution with $n-1$ degrees of freedom.
Step 3 Specify the level of significance $\alpha$.
Step 4 Determine the critical values
For the specified value of $\alpha$ determine the critical region depending upon the alternative hypothesis.
- left-tailed alternative hypothesis: Find the t-critical value using
$$ \begin{aligned} P(t<-t_{\alpha,n-1}) & = \alpha. \end{aligned} $$ - right-tailed alternative hypothesis: $t_\alpha$.
$$ \begin{aligned} P(t>t_{\alpha, n-1}) & = \alpha. \end{aligned} $$ - two-tailed alternative hypothesis: $t_{\alpha/2}$.
$$ \begin{aligned} P(|t| > t_{\alpha/2,n-1}) &= \alpha. \end{aligned} $$
Step 5 Computation
Compute the test statistic under the null hypothesis $H_0$ using equation
$$ \begin{aligned} t_{obs} & = \frac{\overline{x}-\mu_0}{s/\sqrt{n}} \end{aligned} $$
Step 6 Decision (Traditional Approach)
Traditional approach is based on the critical value.
- For left-tailed alternative hypothesis: Reject $H_0$ if
$t_{obs}\leq -t_{\alpha,n-1}$. - right-tailed alternative hypothesis: Reject $H_0$ if
$t_{obs}\geq t_{\alpha,n-1}$. - two-tailed alternative hypothesis: Reject $H_0$ if
$|t_{obs}|\geq t_{\alpha/2, n-1}$.
OR
Step 6 Decision ($p$-value Approach)
It is based on the $p$-value.
| Alternative Hypothesis | Type of Hypothesis | $p$-value |
|---|---|---|
| $H_a: \mu<\mu_0$ | Left-tailed | $p$-value $= P(t\leq t_{obs})$ |
| $H_a: \mu>\mu_0$ | Right-tailed | $p$-value $= P(t\geq t_{obs})$ |
| $H_a: \mu\neq \mu_0$ | Two-tailed | $p$-value $= 2P(t\geq t_{obs})$ |
If p-value is less than $\alpha$, then reject the null hypothesis $H_0$ at $\alpha$ level of significance, otherwise fail to reject $H_0$ at $\alpha$ level of significance.
Let’s understand one sample t test for population mean with the help of numerical examples.
Example 1 One Sample T Test for Population Mean
The Healthy Food Company claims that its cereal boxes contain, on average, 453 grams of cereal. We suspect that the cereal boxes contain, on average, less than claimed. You decided to test the claim by inspecting 6 randomly selected boxes, and get the following weights:
454, 447, 452, 446, 450, 445.
Assume that the amount of cereal in a box follows a normal distribution. Test at 5% level of significance.
Solution
Given that the sample size $n = 6$, sample mean $\overline{x}= 449$ and sample standard deviation $s = 3.578$.
Step 1 Hypothesis Testing Problem
The hypothesis testing problem is
$H_0 : \mu = 453$ against $H_1 : \mu < 453$ ($\text{left-tailed}$)
Step 2 Test Statistic
The test statistic is
$$ \begin{aligned} t& =\frac{\overline{x} -\mu}{s/\sqrt{n}} \end{aligned} $$
which follows $t$ distribution with $n-1$ degrees of freedom.
Step 3 Significance Level
The significance level is $\alpha = 0.05$.
Step 4 Critical Value(s)
As the alternative hypothesis is $\text{left-tailed}$, the t-critical value $\text{is}$ $-2.015$.
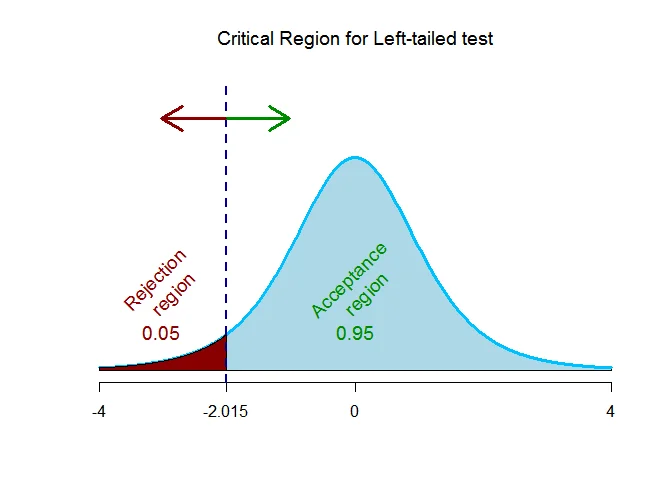
The rejection region (i.e. critical region) is $\text{t < -2.015}$.
Step 5 Computation
The test statistic under the null hypothesis is
$$ \begin{aligned} t&=\frac{ \overline{x} -\mu_0}{s/\sqrt{n}}\\ &= \frac{449-453}{3.578/ \sqrt{6 }}\\ &= -2.738 \end{aligned} $$
Step 6 Decision (Traditional Approach)
The test statistic is $t =-2.738$ which falls $\text{inside}$ the critical region, we $\text{reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value Approach)
This is a $\text{left-tailed}$ test, so the p-value is the area to the left of the test statistic ($t=-2.738$) is p-value = $0.0204$.
The p-value is $0.0204$ which is $\text{less than}$ the significance level of $\alpha = 0.05$, we $\text{reject}$ the null hypothesis.
Example 2 T test critical value calculation
A new brand of laptop battery is produced by a company. The company claims that the battery will last for an extended period of time before a recharge is necessary. A sample of 40 batteries is tested for the length of usage time to recharge. The sample results are as follows:
Sample Size = 40
Sample Mean = 6.5 hrs.
Sample Standard Deviation = 1.3 hrs.
At the 0.01 level of significance, is there evidence that the population mean length of usage is greater than 5.5 hours?
Solution
Given that the sample size $n = 40$, sample mean $\overline{x}= 6.5$ and sample standard deviation $s = 1.3$.
Step 1 Hypothesis Testing Problem
The hypothesis testing problem is
$H_0 : \mu = 5.5$ against $H_1 : \mu > 5.5$ ($\text{right-tailed}$)
Step 2 Test Statistic
The test statistic is
$$ \begin{aligned} t& =\frac{\overline{x} -\mu}{s/\sqrt{n}} \end{aligned} $$
which follows $t$ distribution with $n-1$ degrees of freedom.
Step 3 Significance Level
The significance level is $\alpha = 0.01$.
Step 4 Critical Value(s)
As the alternative hypothesis is $\text{right-tailed}$, the t test critical value $\text{is}$ $2.426$.
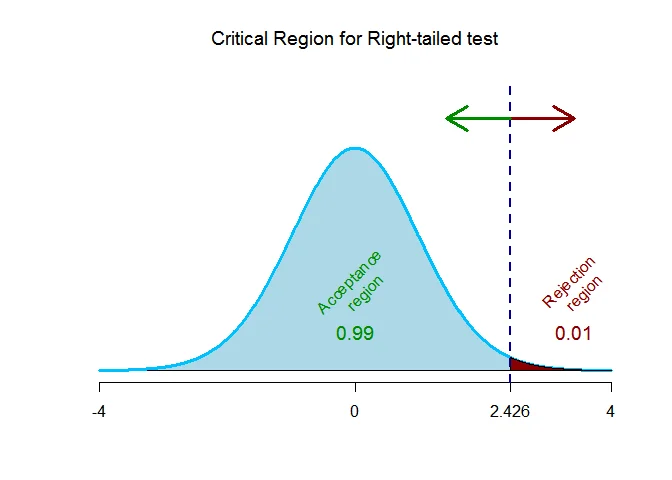
The rejection region (i.e. critical region) is $\text{t > 2.426}$.
Step 5 Computation
The test statistic under the null hypothesis is
$$ \begin{aligned} t&=\frac{ \overline{x} -\mu_0}{s/\sqrt{n}}\\ &= \frac{6.5-5.5}{1.3/ \sqrt{40 }}\\ &= 4.865 \end{aligned} $$
Step 6 Decision (Traditional Approach)
The test statistic is $t =4.865$ which falls $\text{inside}$ the critical region, we $\text{reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value Approach)
This is a $\text{right-tailed}$ test, so the p-value is the area to the left of the test statistic ($t=4.865$) is p-value = $0$.
The p-value is $0$ which is $\text{less than}$ the significance level of $\alpha = 0.01$, we $\text{reject}$ the null hypothesis.
Example 3 T-test for one mean
A special cable manufactured by a company has a breaking strength of 800 pounds. (Assume the breaking strength is normally distributed.) A researcher selects a random sample of 20 cables and finds the average breaking strength is 793 pounds with a standard deviation of 12 pounds. Do these data support the claim that the average breaking strength is not 800 pounds? Test at the 0.05 level of significance.
Solution
Given that the sample size $n = 20$, sample mean $\overline{x}= 793$ and sample standard deviation $s = 12$.
Step 1 Hypothesis Testing Problem
The hypothesis testing problem is
$H_0 : \mu = 800$ against $H_1 : \mu \neq 800$ ($\text{two-tailed}$)
Step 2 Test Statistic
The test statistic is
$$ \begin{aligned} t& =\frac{\overline{x} -\mu}{s/\sqrt{n}} \end{aligned} $$
which follows $t$ distribution with $n-1$ degrees of freedom.
Step 3 Significance Level
The significance level is $\alpha = 0.05$.
Step 4 Critical Value(s)
As the alternative hypothesis is $\text{two-tailed}$, the critical value of $t$ $\text{are}$ $-2.093$ and $2.093$.
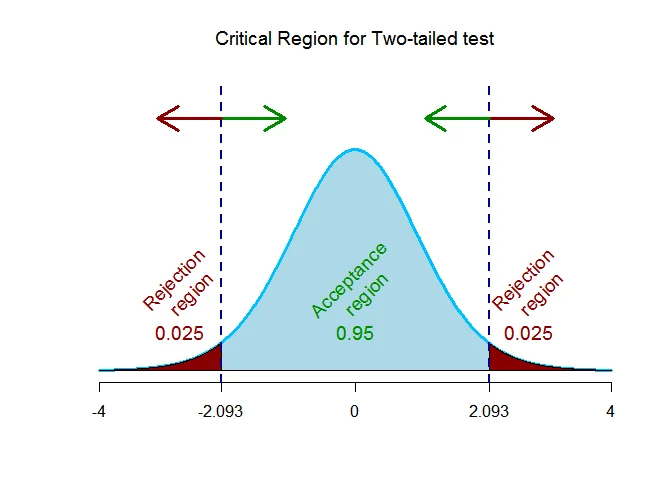
The rejection region (i.e. critical region) is $\text{t < -2.093 or t > 2.093}$.
Step 5 Computation
The test statistic under the null hypothesis is
$$ \begin{aligned} t&=\frac{ \overline{x} -\mu_0}{s/\sqrt{n}}\\ &= \frac{793-800}{12/ \sqrt{20 }}\\ &= -2.609 \end{aligned} $$
Step 6 Decision (Traditional Approach)
The test statistic is $t =-2.609$ which falls $\text{inside}$ the critical region, we $\text{reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value Approach)
This is a $\text{two-tailed}$ test, so the p-value is the area to the left of the test statistic ($t=-2.609$) is p-value = $0.0173$.
The p-value is $0.0173$ which is $\text{less than}$ the significance level of $\alpha = 0.05,$ we $\text{reject}$ the null hypothesis.
Conclusion
I hope this tutorial will help you to understand how to solve the numerical problems based on one-sample t-test for population mean. You can read more about paired t test calculator and chi-square test for variance calculator