Binomial Distribution
In this tutorial, we will provide you step by step solution to some numerical examples on Binomial distribution to make sure you understand the Binomial distribution clearly and correctly.
Upon successful completion of this tutorial, you will be able to understand how to calculate binomial probabilities.
Definition of Binomial Distribution
A discrete random variable $X$ is said to have Binomial distribution with parameters $n$ and $p$ if the probability mass function of $X$ is
$$ \begin{eqnarray*} P(X=x) & =& \binom{n}{x} p^x q^{n-x},\\ & & \qquad \; x = 0,1,2, \cdots, n; \;\\ & & 0 \leq p \leq 1, q = 1-p \end{eqnarray*} $$
where,
- $n =$ number of trials,
- $X =$ number of successes in $n$ trials,
- $p =$ probability of success,
- $q = 1- p =$ probability of failures.
Mean of Binomial Distribution
The mean or expected value of binomial random variable $X$ is $E(X) = np$.
Variance of Binomial distribution
The variance of Binomial random variable $X$ is $V(X) = npq$.
Example 1
Suppose that a short quiz consists of 6 multiple choice questions.Each question has four possible answers of which ony one in correct. A student guesses on every question. Find the probability that a student will answer
a. five or more quetions correctly,
b. all questions correctly,
c. at most 1 questions correctly,
d. between 4 and 5 (inclusive) questions correctly.
Solution
Let $X$ be the number of questions guessed correctly out of $6$ questions. Let $p$ be the probability of correct guess.
The random variable $X$ follows a Binomial distribution with parameter $n=6$ and $p=0.25$. That is, $X\sim B(6, 0.25)$.
The probability mass function of $X$ is
$$ \begin{aligned} P(X=x) &= \binom{6}{x} (0.25)^x (1-0.25)^{6-x}, \; x=0,1,\cdots, 6\\ &=\binom{6}{x} (0.25)^x (0.75)^{6-x}, \; x=0,1,\cdots,6 \end{aligned} $$
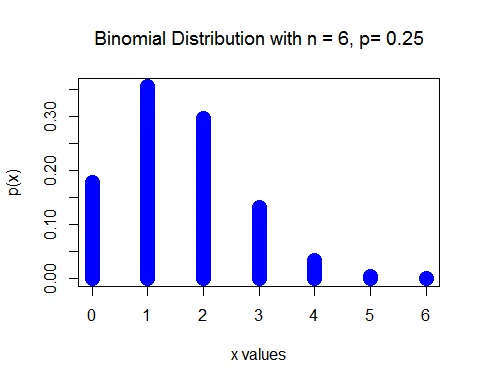
a. The probability that a student will answer $5$ or more questions correctly is
$$ \begin{aligned} P(X\geq 5) &= P(X=5)+P(X=6)\\ &= \binom{6}{5} (0.25)^{5} (0.75)^{6-5}+\binom{6}{6} (0.25)^{6} (0.75)^{6-6}\\ &= 0.0044+0.0002\\ & = 0.0046 \end{aligned} $$
b. The probability that a student will answer all questions correctly is
$$ \begin{aligned} P(X= 6) & =P(6)\\ &= \binom{6}{6} (0.25)^{6} (0.75)^{6-6}\\ & = 0.0002 \end{aligned} $$
c. The probability that a student will answer at most $1$ questions correctly is
$$ \begin{aligned} P(X\leq 1) &= P(X=0)+P(X=1)\\ &= \binom{6}{0} (0.25)^{0} (0.75)^{6-0}+\binom{6}{1} (0.25)^{1} (0.75)^{6-1}\\ &=0.178+0.356\\ &= 0.5339 \end{aligned} $$
d. The probability that a student will answer between $4$ and $5$ questions correctly is
$$ \begin{aligned} P(4\leq X\leq 5) & =P(X=4)+P(X=5)\\ &= \binom{6}{4} (0.25)^{4} (0.75)^{6-4}+\binom{6}{5} (0.25)^{5} (0.75)^{6-5}\\ & = 0.033+0.0044\\ &= 0.0374 \end{aligned} $$
Example 2
35% of the adults says cashews are their favorite kind of nuts. If you randomly select 10 adults and ask each adult to name his or her favorite nut, compute the probability that the number of adults who say cashews are their favorite nut is
a. exactly 4,
b. less than 3,
c. at least 3,
d. at the most 2.
Solution
Let $X$ be the number of adults out of $10$ who say cashew is their favorite nut.
Let $p$ be the probability that an adults favorite nut is cashew.
Given that $p=0.35$ and $n =10$. Here $X$ follows a Binomial distribution. That is, $X\sim B(10, 0.35)$.
The probability mass function of $X$ is
$$ P(X=x) = \binom{10}{x} (0.35)^x (1-0.35)^{10-x}, \; x=0,1,\cdots, 10. $$
The mean of $X$ is
$$ \begin{aligned} \mu =E(X) &= n*p\\ &= 10*0.35\\ &= 3.5 \end{aligned} $$
and the standard deviation of $X$ is
$$ \begin{aligned} \sigma=\sqrt{V(X)} &=\sqrt{n*p*(1-p)}\\ &=\sqrt{10*0.35* (1- 0.35)}\\ &= 1.5083 \end{aligned} $$
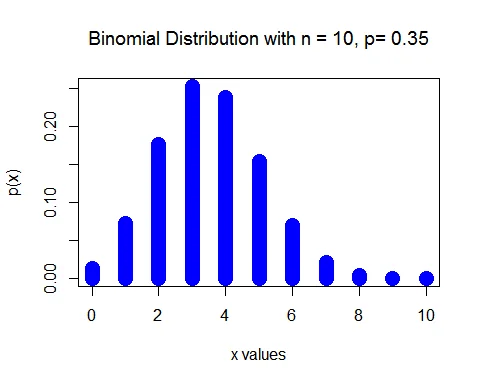
a. The probability that exactly 4 adults say cashews are their favorite nut is
$$ \begin{aligned} P(X= 4) & =P(4)\\ &= \binom{10}{4} (0.35)^{4} (1-0.35)^{10-4}\\ &= 210\times 0.015\times 0.0754\\ & = 0.2377 \end{aligned} $$
b. The probability that less than 3 adults say cashews are their favorite nut is
$$ \begin{aligned} P(X< 3) & =P(X\leq 2)\\ &= P(0)+P(1)\\ & = 0.0135+0.0725\\ & = 0.2616 \end{aligned} $$
c. The probability that at least 3 adults say cashews are their favorite nut is
$$ \begin{aligned} P(X\geq 3) & =1-P(X\leq 2)\\ &= 1-(P(0)+P(1))\\ & = 1-\big(0.0135+0.0725 \big)\\ & = 0.7384 \end{aligned} $$
d. The probability that at most 2 adults say cashews are their favorite nut is
$$ \begin{aligned} P(X\leq 2) & =\sum_{x=0}^{2} P(x)\\ & =P(0) + P(1) + P(2)\\ & = 0.0135+0.0725+0.1757\\ &= 0.2616 \end{aligned} $$

