Introduction
Binomial distribution is one of the most important discrete distribution in statistics. In this tutorial we will discuss about theory of Binomial distribution along with proof of some important results related to binomial distribution.
Binomial Experiment
Binomial experiment is a random experiment that has following properties:
- The random experiment consists of n repeated Bernoulli trial.
- Each trial has only two possible outcomes like success ($S$) and failure ($F$).
- All the trials are independent, i.e. the results of any trial is not affected by the preceding trials and does not affect the outcomes of succeeding trials.
- The probability of success $p$ is constant for each trial.
- The random variable $X$ is the total number of successes in $n$ trials.
In short Binomial Experiment is the repetition of independent Bernoulli trials finite number of times.
Binomial Distribution
Consider a series of $n$ (finite) independent Bernoulli trials. Let $p$ be the probability of success in each Bernoulli trial. Let $q=1-p$ be the probability of failure in each Bernoulli trial. The probability of success remains constant from one trial to another.
Let $X$ denote the number of successes in $n$ trials. Then the random variable $X$ take the values $X = 0,1,2,\cdots,n$.
The number of ways of getting $x$ successes out of $n$ trials is $\binom{n}{x}$, where $\binom{n}{x} =\dfrac{n!}{x!(n-x)!}$.
Hence the probability of getting $x$ successes (and $n-x$ failures) in $n$ trials is
$$ \begin{eqnarray*} P(X=x) &=& \binom{n}{x}p\cdot p \cdots (x \text{ times})\times q\cdot q \cdots ((n-x)\text{ times}) \\ &=& \binom{n}{x} p^x q^{n-x}. \end{eqnarray*} $$
Hence, the probability distribution of random variable $X$ is
$$ \begin{eqnarray*} P(X=x) & =& \binom{n}{x} p^x q^{n-x},\\ & & \qquad \; x = 0,1,2, \cdots, n; \;\\ & & 0 \leq p \leq 1, q = 1-p \end{eqnarray*} $$
where
- $n =$ number of trials,
- $X =$ number of successes in $n$ trials,
- $p =$ probability of success,
- $q = 1- p =$ probability of failures.
The above distribution is called Binomial distribution. The name Binomial distribution is given because various probabilities are the terms from the Binomial expansion
$$ (a+b)^n =\sum_{i=1}^n\binom{n}{i} a^i b^{n-i}. $$
Clearly,
a. $P(X=x)\geq 0$ for all $x$ and
b. $\sum_{x=0}^n P(X=x)=1$.
Hence, $P(X=x)$ defined above is a legitimate probability mass function.
Notations: $X \sim B(n,p)$.
Examples of Binomial Random Variable
- Number of heads when tossing a coin 8 times.
- Number of correct guesses at 20 True/False questions.
- Number of correct guesses at 15 multiple choice questions each one correct option out of four options.
Definition
A discrete random variable $X$ is said to have Binomial distribution with parameter $n$ and $p$ if its probability mass function is
$$ \begin{equation*} P(X=x)= \left\{ \begin{array}{ll} \binom{n}{x} p^x q^{n-x}, & \hbox{$x=0,1,2,\cdots, n$;} \\ & \hbox{$0<p<1, q=1-p$} \\ 0, & \hbox{Otherwise.} \end{array} \right. \end{equation*} $$
Key features of Binomial distribution
- The random experiment consists of n repeated Bernoulli trial.
- Each trial has only two possible outcomes like success ($S$) and failure ($F$).
- All the trials are independent, i.e. the results of any trial is not affected by the preceding trials and does not affect the outcomes of succeeding trials.
- The probability of success $p$ is constant for each trial.
- The random variable $X$ is the total number of successes in $n$ trials.
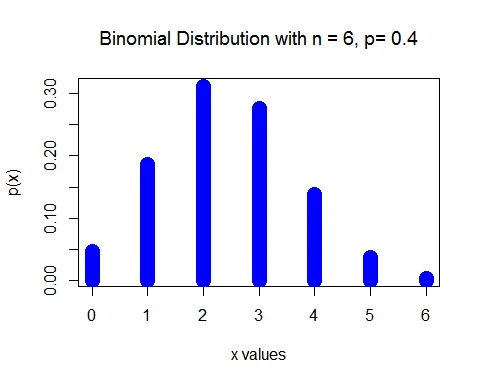
Graph of Binomial Distribution
Graph of Binomial distribution with parameter $n=6$ and $p=0.4$ is
Mean of Binomial Distribution
The mean or expected value of binomial random variable $X$ is $E(X) = np$.
Proof
The mean of binomial random variable $X$ is
$$ \begin{eqnarray*} E(X) &=& \sum_{x=0}^n x\cdot P(X=x)\\ &=& \sum_{x=0}^n x\cdot \binom{n}{x} p^x q^{n-x}\\ &=& \sum_{x=0}^n x\frac{n!}{x!(n-x)!}p^x q^{n-x}\\ &=& 0+\sum_{x=1}^n \frac{n(n-1)!}{(x-1)!(n-x)!}p^x q^{n-x}\\ &=& np\sum_{x=1}^n \frac{(n-1)!}{(x-1)!(n-x)!}p^{x-1} q^{n-x}\\ &=& np\sum_{x=1}^n \binom{n-1}{x-1}p^{x-1}q^{n-x}\\ &=& np\cdot (q+p)^{n-1}\\ &=& np. \end{eqnarray*} $$
Variance of Binomial distribution
The variance of Binomial random variable $X$ is $V(X) = npq$.
Proof
The variance of random variable $X$ is given by
$$ V(X) = E(X^2) - [E(X)]^2 $$
Let us find the expected value $X^2$.
$$ \begin{eqnarray*} E(X^2) & = & E[X(X-1)+X]\\ &=& E[X(X-1)] + E(X)\\ &=& \sum_{x=0}^n x(x-1)\cdot P(X=x)+ np\\ &=& \sum_{x=0}^n x(x-1)\cdot \binom{n}{x} p^x q^{n-x}+np\\ &=& \sum_{x=0}^n x(x-1)\frac{n!}{x!(n-x)!}p^x q^{n-x}+np\\ &=& 0+0+\sum_{x=2}^n \frac{n(n-1)(n-2)!}{(x-2)!(n-x)!}p^x q^{n-x}+np\\ &=& n(n-1)p^2\sum_{x=2}^n \frac{(n-2)!}{(x-2)!(n-x)!}p^{x-2} q^{n-x}+np\\ &=& n(n-1)p^2\sum_{x=2}^n \binom{n-2}{x-2}p^{x-2}q^{n-x}+np\\ &=& n(n-1)p^2(q+p)^{n-2}+ np, \\ &=& n(n-1)p^2+ np. \end{eqnarray*} $$
Thus, variance of Binomial random variable $X$ is
$$ \begin{eqnarray*} V(X) &= & E(X^2) - [E(X)]^2\\ &=& n(n-1)p^2+ np-(np)^2\\ &=& np-np^2\\ &=& np(1-p)\\ &=& npq \end{eqnarray*} $$
For Binomial distribution, Mean > Variance.
Moment Generating Function of Binomial Distribution
The moment generating function (MGF) of Binomial distribution is given by
$$ M_X(t) = (q+pe^t)^n.$$
Proof
Let $X\sim B(n,p)$ distribution. Then the MGF of $X$ is
$$ \begin{eqnarray*} M_X(t) &=& E(e^{tx}) \\ &=& \sum_{x=0}^n e^{tx}\binom{n}{x} p^x q^{n-x} \\ &=& \sum_{x=0}^n \binom{n}{x} (pe^t)^x q^{n-x} \\ &=& (q+pe^t)^n. \end{eqnarray*} $$
Cumulant Generating Function of Binomial Distribution
The cumulant generating function of Binomial random variable $X$ is $K_X(t) = n\log_e (q+pe^t)$.
Proof
Let $X\sim B(n,p)$ distribution. Then the CGF of $X$ is
$$ \begin{equation*} K_X(t) = \log_e M_X(t) = n\log_e(q+pe^t). \end{equation*} $$
Recurrence relation for cumulants
The recurrence relation for cumulants of Binomial distribution is
$$ \begin{equation*} \kappa_{r+1} = pq \frac{d\kappa_r}{dp}. \end{equation*} $$
Proof
The $r^{th}$ cumulant is given by
$$ \begin{eqnarray*} \kappa_r & = & \bigg[\frac{d^r}{dt^r} K_X(t)\bigg]_{t=0}\\ & = & \bigg[\frac{d^r}{dt^r} n\log_e(q+pe^t)\bigg]_{t=0}. \end{eqnarray*} $$
Differentiating $\kappa_r$ with respect to $p$, we have
$$ \begin{eqnarray*} \frac{d \kappa_r}{dp} &=& n\bigg[\frac{d^r}{dt^r} \frac{d}{dp} \log_e(q+pe^t)\bigg]_{t=0} \\ &=& n\bigg[\frac{d^r}{dt^r} \bigg(\frac{e^t-1}{q+pe^t}\bigg) \bigg]_{t=0}. \end{eqnarray*} $$
Also, the $(r+1)^{th}$ cumulant is given by
$$ \begin{eqnarray*} \kappa_{r+1} & = & \bigg[\frac{d^{r+1}}{dt^{r+1}} K_X(t)\bigg]_{t=0}\\ &=& \bigg[\frac{d^{r+1}}{dt^{r+1}} n\log_e(q+pe^t)\bigg]_{t=0}\\ &=& \bigg[\frac{d^r}{dt^r} \bigg\{\frac{d}{dt} n\log_e(q+pe^t)\bigg\}\bigg]_{t=0}\\ &=& n\bigg[\frac{d^{r}}{dt^{r}}\bigg(\frac{pe^t}{q+pe^t}\bigg)\bigg]_{t=0}. \end{eqnarray*} $$
Hence,
$$ \begin{eqnarray*} \kappa_{r+1}-pq \frac{d \kappa_r}{dp} &=& n\bigg[\frac{d^{r}}{dt^{r}}\bigg(\frac{pe^t-pqe^t+pq}{q+pe^t}\bigg)\bigg]_{t=0}\\ &=& n\bigg[\frac{d^{r}}{dt^{r}}\bigg(\frac{p(pe^t+q}{q+pe^t}\bigg)\bigg]_{t=0}.\\ &=& n\bigg[\frac{d^{r}}{dt^{r}}(p)\bigg]_{t=0}=0. \end{eqnarray*} $$
Hence, the recurrence relation for cumulants is
$$ \begin{equation*} \kappa_{r+1}=pq \frac{d \kappa_r}{dp}. \end{equation*} $$
Probability Generating Function of Binomial Distribution
The probability generating function (PGF) of Binomial distribution is given by
$$ P_X(t) = (q+pt)^n.$$
Proof
Let $X\sim B(n,p)$ distribution. Then the probability generating function of $X$ is
$$ \begin{eqnarray*} P_X(t) &=& E(t^x) \\ &=& \sum_{x=0}^n t^x\binom{n}{x} p^x q^{n-x} \\ &=& \sum_{x=0}^n \binom{n}{x} (pt)^x q^{n-x} \\ &=& (q+pt)^n. \end{eqnarray*} $$
Characteristics Function of Binomial Distribution
The characteristics function of Binomial distribution is given by
$$\phi_X(t) = (q+pe^{it})^n.$$
Proof
Let $X\sim B(n,p)$ distribution. Then the characteristics function of $X$ is
$$ \begin{eqnarray*} \phi_X(t) &=& E(e^{itx}) \\ &=& \sum_{x=0}^n e^{itx}\binom{n}{x} p^x q^{n-x} \\ &=& \sum_{x=0}^n \binom{n}{x} (pe^{it})^x q^{n-x} \\ &=& (q+pe^{it})^n. \end{eqnarray*} $$
Binomial distribution as a sum of Bernoulli distributions
If $X_1,X_2,\cdots, X_n$ are independent Bernoulli distributed random variables with parameter $p$, then the random variable $X$ defined by $X=X_1+X_2+\cdots + X_n$ has a Binomial distribution with parameter $n$ and $p$.
Proof
Let $X_i \sim Bernoulli(p)$. All $X_i$ are independently distributed.
Then the MGF of $X$ is
$$ \begin{equation*} M_{X_i}(t) = (q+pe^t). \end{equation*} $$
Let $X=X_1+X_2+\cdots + X_n$.
Then the MGF of $X$ is
$$ \begin{eqnarray*} M_X(t) &=& E(e^{tX}) \\ &=& E(e^{t(X_1+X_2+\cdots + X_n)}) \\ &=& E\big[\prod_{i=1}^{n} e^{tX_i} \big] \\ &=& \prod_{i=1}^{n} E(e^{tX_i})\qquad (\because X_1, X_2 \text{ are independent })\\ &=& \prod_{i=1}^{n} M_{X_i}(t)\\ &=& \prod_{i=1}^{n}(q+pe^t)\\ &=& (q+pe^t)^{n}. \end{eqnarray*} $$
which is the MGF of Binomial variate with parameter $n$ and $p$. Hence, by uniqueness theorem of moment generating function $X=X_1+X_2+\cdots +X_n\sim B(n, p)$.
Additive Property of Binomial Distribution
Let $X_1$ and $X_2$ be two independent Binomial variate with parameters $(n_1, p)$ and $(n_2, p)$ respectively. Then $Y=X_1+X_2\sim B(n_1+n_2, p)$.
Proof
Let $X_1$ and $X_2$ be two independent Binomial variate with parameters $(n_1, p)$ and $(n_2, p)$ respectively. Let $Y=X_1+X_2$. Then the m.g.f. of $Y$ is
$$ \begin{eqnarray*} M_Y(t) &=& E(e^{tY}) \\ &=& E(e^{t(X_1+X_2)}) \\ &=& E(e^{tX_1} e^{tX_2}) \\ &=& E(e^{tX_1})\cdot E(e^{tX_2})\qquad (\because X_1, X_2 \text{ are independent })\\ &=& M_{X_1}(t)\cdot M_{X_2}(t)\\ &=& (q+pe^t)^{n_1}(q+pe^t)^{n_2}\\ &=& (q+pe^t)^{n_1+n_2}. \end{eqnarray*} $$
which is the m.g.f. of Binomial variate with parameter $n_1+n_2$ and $p$. Hence, by uniqueness theorem of moment generating function $Y=X_1+X_2\sim B(n_1+n_2, p)$.
Recurrence relation for raw moments
The recurrence relation for raw moments of Binomial distribution is
$$ \begin{equation*} \mu_{r+1}^\prime = p \bigg[ q\frac{d\mu_r^\prime}{dp} + n\mu_r^\prime\bigg]. \end{equation*} $$
Recurrence relation for central moments
The recurrence relation for central moments of Binomial distribution is
$$ \begin{equation*} \mu_{r+1} = pq \bigg[ \frac{d\mu_r}{dp} + nr\mu_{r-1}\bigg]. \end{equation*} $$
Recurrence relation for probabilities
The recurrence relation for probabilities of Binomial distribution is
$$ \begin{equation*} P(X=x+1) = \frac{n-x}{x+1}\cdot \frac{p}{q}\cdot P(X=x), \; x=0,1,2\cdots, n-1. \end{equation*} $$
If $X\sim B(n,p)$ distribution then $Y = X-n\sim B(n,1-p)$ distriution.

