Discrete Uniform Distribution
A discrete random variable has a discrete uniform distribution if each value of the random variable is equally likely and the values of the random variable are uniformly distributed throughout some specified interval.
In this article, I will walk you through discrete uniform distribution and proof related to discrete uniform. You can use discrete uniform distribution Calculator.
Discrete Uniform Distribution Definition
A discrete random variable $X$ is said to have a uniform distribution if its probability mass function (pmf) is given by
$$ \begin{aligned} P(X=x)&=\frac{1}{N},;; x=1,2, \cdots, N. \end{aligned} $$
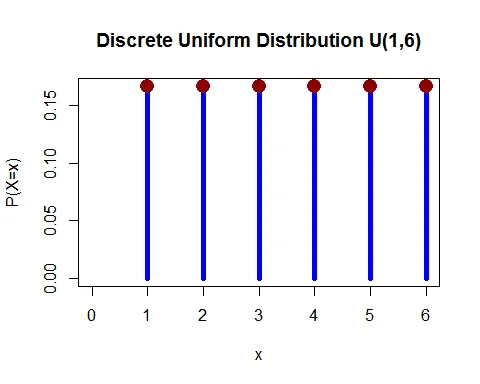
Discrete Uniform Distribution Graph
Following graph shows the probability mass function (pmf) of discrete uniform distribution $U(1,6)$.
Mean of Discrete Uniform Distribution
How do you find mean of discrete uniform distribution? is given below with proof
The expected value of discrete uniform random variable is $E(X) =\dfrac{N+1}{2}$.
Proof
The expected value of discrete uniform random variable is
$$ \begin{aligned} E(X) &= \sum_{x=1}^N x\cdot P(X=x)\\ &= \frac{1}{N}\sum_{x=1}^N x\\ &= \frac{1}{N}(1+2+\cdots + N)\\ &= \frac{1}{N}\times \frac{N(N+1)}{2}\\ &= \frac{N+1}{2}. \end{aligned} $$
Hence, the mean of discrete uniform distribution is $E(X) =\dfrac{N+1}{2}$.
Variance of Discrete Uniform Distribution
The variance of discrete uniform random variable is $V(X) = \dfrac{N^2-1}{12}$.
Proof
The discrete uniform distribution variance proof for random variable $X$ is given by
$$ \begin{equation*} V(X) = E(X^2) - [E(X)]^2. \end{equation*} $$
Let us find the expected value of $X^2$.
$$ \begin{eqnarray*} E(X^2) &=& \sum_{x=1}^N x^2\cdot P(X=x)\\ &=& \frac{1}{N}\sum_{x=1}^N x^2\\ &=& \frac{1}{N}(1^2+2^2+\cdots + N^2)\\ &=& \frac{1}{N}\times \frac{N(N+1)(2N+1)}{6}\\ &=& \frac{(N+1)(2N+1)}{6}. \end{eqnarray*} $$
Now, the variance of $X$ is
$$ \begin{eqnarray*} V(X) & = & E(X^2) - [E(X)]^2\\ &=& \frac{(N+1)(2N+1)}{6}- \bigg(\frac{N+1}{2}\bigg)^2\\ &=& \frac{N+1}{2}\bigg[\frac{2N+1}{3}-\frac{N+1}{2} \bigg]\\ &=& \frac{N+1}{2}\bigg[\frac{4N+2-3N-3}{6}\bigg]\\ &=& \frac{N+1}{2}\bigg[\frac{N-1}{6}\bigg]\\ &=& \frac{N^2-1}{12}. \end{eqnarray*} $$
Thus the variance of discrete uniform distribution is $\sigma^2 =\dfrac{N^2-1}{12}$.
The discrete uniform distribution standard deviation is $\sigma =\sqrt{\dfrac{N^2-1}{12}}$.
Discrete uniform distribution Moment generating function (MGF)
MGF of discrete uniform distribution is given by The MGF of $X$ is $M_X(t) = \dfrac{e^t (1 - e^{tN})}{N (1 - e^t)}$.
Proof
Discrete uniform distribution moment generating function proof is given as below
The moment generating function (MGF) of random variable $X$ is
$$ \begin{eqnarray*} M(t) &=& E(e^{tx})\\ &=& \sum_{x=1}^N e^{tx} \dfrac{1}{N} \\ &=& \dfrac{1}{N} \sum_{x=1}^N (e^t)^x \\ &=& \dfrac{1}{N} e^t \dfrac{1-e^{tN}}{1-e^t} \\ &=& \dfrac{e^t (1 - e^{tN})}{N (1 - e^t)}. \end{eqnarray*} $$
General discrete uniform distribution
A general discrete uniform distribution has a probability mass function
$$ \begin{aligned} P(X=x)&=\frac{1}{b-a+1},;; x=a,a+1,a+2, \cdots, b. \end{aligned} $$
Mean of General discrete uniform distribution
The expected value of discrete uniform random variable is $E(X) =\dfrac{a+b}{2}$.
Variance of General discrete uniform distribution
The variance of above discrete uniform random variable is $V(X) = \dfrac{(b-a+1)^2-1}{12}$.
Distribution Function of General discrete uniform distribution
The distribution function of general discrete uniform distribution is
$F(x) = P(X\leq x)=\frac{x-a+1}{b-a+1}; a\leq x\leq b$.
Below are the few solved example on Discrete Uniform Distribution with step by step guide on how to find probability and mean or variance of discrete uniform distribution.
Discrete Uniform Distribution Example 1
Roll a six faced fair die. Suppose $X$ denote the number appear on the top of a die.
a. Find the probability that an even number appear on the top, b. Find the probability that the number appear on the top is less than 3. c. Compute mean and variance of $X$.
Solution
Let $X$ denote the number appear on the top of a die. Then the random variable $X$ take the values $X=1,2,3,4,5,6$ and $X$ follows $U(1,6)$ distribution.
The probability mass function (pmf) of random variable $X$ is
$$ \begin{aligned} P(X=x)&=\frac{1}{6-1+1}\\ &=\frac{1}{6}, \; x=1,2,\cdots, 6. \end{aligned} $$
a. The probability that an even number appear on the top of the die is
$$ \begin{aligned} P(X=\text{ even number }) &=P(X=2)+P(X=4)+P(X=6)\\ &=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}\\ &=\frac{3}{6}\\ &= 0.5 \end{aligned} $$
b. The probability that the number appear on the top of the die is less than 3 is
$$ \begin{aligned} P(X < 3) &=P(X=1)+P(X=2)\\ &=\frac{1}{6}+\frac{1}{6}\\ &=\frac{2}{6}\\ &= 0.3333 \end{aligned} $$
c. The mean of discrete uniform distribution $X$ is
$$ \begin{aligned} E(X) &=\frac{1+6}{2}\\ &=\frac{7}{2}\\ &= 3.5 \end{aligned} $$
The variance of discrete uniform distribution $X$ is
$$ \begin{aligned} V(X) &=\frac{(6-1+1)^2-1}{12}\\ &=\frac{35}{12}\\ &= 2.9167 \end{aligned} $$
Hope you like article on Discrete Uniform Distribution. You can refer below recommended articles for discrete uniform distribution calculator.
