Continuous Uniform Distribution
A random variable has a uniform distribution if each value of the random variable is equally likely and the values of the random variable are uniformly distributed throughout some specified interval. A uniform distribution is a distribution with constant probability.
This tutorial will help you understand the theory and proof of theoretical results of uniform distribution.
Uniform distribution is also known as rectangular distribution (see the graph below).
Definition of Uniform Distribution
A continuous random variable $X$ is said to have a Uniform distribution (or rectangular distribution) with parameters $\alpha$ and $\beta$ if its p.d.f. is given by
$$ \begin{equation*} f(x)=\left\{ \begin{array}{ll} \frac{1}{\beta - \alpha}, & \hbox{$\alpha \leq x\leq \beta$;} \\ 0, & \hbox{Otherwise.} \end{array} \right. \end{equation*} $$
Notation: $X\sim U(\alpha, \beta)$.
Clearly,
$f(x)\geq 0$ for all $\alpha \leq x\leq \beta$ and
$$ \begin{eqnarray*} \int_\alpha^\beta f(x) \; dx &=& \int_\alpha^\beta \frac{1}{\beta-\alpha}\;dx\\ &=& \frac{1}{\beta - \alpha}\int_\alpha^\beta \;dx\\ &=& \frac{1}{\beta - \alpha}\big[x\big]_\alpha^\beta \\ &=& \frac{\beta-\alpha}{\beta - \alpha}\\ &=& 1. \end{eqnarray*} $$
Hence $f(x)$ defined above is a legitimate probability density function.
Graph of Uniform Distribution
Following is the graph of probability density function of continuous uniform (rectangular) distribution with parameters $\alpha=1$ and $\beta =5$.
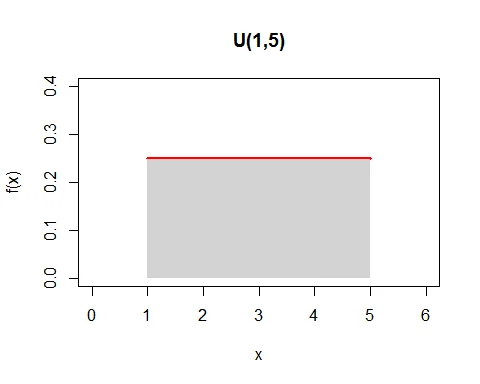
Note that the base of the rectangle is $\beta-\alpha$ and the length of height of the rectangle is $\dfrac{1}{\beta-\alpha}$. So the area under the $f(x)$ is $(\beta-\alpha)*\dfrac{1}{\beta-\alpha}=1$. Hence, $f(x)$ is the legitimate probability density function.
Standard Uniform Distribution
The case where $\alpha=0$ and $\beta=1$ is called standard uniform distribution. The probability density of standard uniform distribution $U(0,1)$ is
$$ \begin{equation*} f(x)=\left\{ \begin{array}{ll} 1, & \hbox{$0 \leq x\leq 1$;} \\ 0, & \hbox{Otherwise.} \end{array} \right. \end{equation*} $$
Distribution Function
The distribution function of uniform distribution $U(\alpha,\beta)$ is
$$ \begin{equation*} F(x)=\left\{ \begin{array}{ll} 0, & \hbox{$x<\alpha$;}\\ \dfrac{x-\alpha}{\beta - \alpha}, & \hbox{$\alpha \leq x\leq \beta$;} \\ 1, & \hbox{$x>\beta$;} \end{array} \right. \end{equation*} $$
Proof
The distribution function of uniform distribution is
$$ \begin{eqnarray*} F(x) &=& P(X\leq x) \\ &=& \int_\alpha^x f(x)\;dx\\ &=& \dfrac{1}{\beta - \alpha}\int_\alpha^x \;dx\\ &=& \dfrac{1}{\beta - \alpha}\big[x\big]_\alpha^x \\ &=& \dfrac{x-\alpha}{\beta - \alpha}. \end{eqnarray*} $$
Thus the distribution function of uniform distribution is
$$ \begin{equation*} F(x)=\left\{ \begin{array}{ll} 0, & \hbox{$x<\alpha$;}\\ \dfrac{x-\alpha}{\beta - \alpha}, & \hbox{$\alpha \leq x\leq \beta$;} \\ 1, & \hbox{$x>\beta$.} \end{array} \right. \end{equation*} $$
Mean of Uniform Distribution
The mean of uniform distribution is $E(X) = \dfrac{\alpha+\beta}{2}$.
Proof
The expected value of uniform distribution is
$$ \begin{eqnarray*} E(X) &=& \int_{\alpha}^\beta xf(x) \; dx\\ &=& \int_{\alpha}^\beta x\frac{1}{\beta-\alpha}\; dx\\ &=& \frac{1}{\beta-\alpha} \bigg[\frac{x^2}{2}\bigg]_\alpha^\beta\\ &=& \frac{1}{\beta-\alpha} \big(\frac{\beta^2}{2}-\frac{\alpha^2}{2}\big)\\ &=& \frac{1}{\beta-\alpha} \cdot\frac{\beta^2-\alpha^2}{2}\\ &=& \frac{1}{\beta-\alpha} \cdot\frac{(\beta-\alpha)(\beta+\alpha)}{2}\\ &=& \frac{\alpha+\beta}{2} \end{eqnarray*} $$
Variance of Uniform Distribution
The variance of uniform distribution is $V(X) = \dfrac{(\beta - \alpha)^2}{2}$.
Proof
The variance of random variable $X$ is given by
$$ \begin{equation*} V(X) = E(X^2) - [E(X)]^2. \end{equation*} $$
Let us find the expected value of $X^2$.
$$ \begin{eqnarray*} E(X^2) &=& \int_{\alpha}^\beta x^2\frac{1}{\beta-\alpha}\; dx\\ &=& \frac{1}{\beta-\alpha} \bigg[\frac{x^3}{3}\bigg]_\alpha^\beta\\ &=& \frac{1}{\beta-\alpha} \bigg[\frac{\beta^3-\alpha^3}{3}\bigg]\\ &=& \frac{1}{\beta-\alpha} \cdot\frac{(\beta-\alpha)(\beta^2+\alpha\beta +\alpha^2)}{3}\\ &=& \frac{\beta^2+\alpha\beta +\alpha^2}{3} \end{eqnarray*} $$
Thus, variance of $X$ is
$$ \begin{eqnarray*} V(X) &=&E(X^2) - [E(X)]^2\\ &=&\frac{\beta^2+\alpha\beta +\alpha^2}{3}-\bigg(\frac{\alpha+\beta}{2}\bigg)^2\\ &=& \frac{\beta^2+\alpha\beta +\alpha^2}{3}-\frac{\alpha^2+2\alpha\beta+ \beta^2}{4}\\ &=& \frac{4(\beta^2+\alpha\beta +\alpha^2)-3(\alpha^2+2\alpha\beta+ \beta^2)}{12}\\ &=&\frac{(\beta^2-2\alpha\beta + \alpha^2)}{12}\\ &=&\frac{(\beta-\alpha)^2}{12}. \end{eqnarray*} $$
Standard deviation of uniform distribution is $\sigma =\sqrt{\dfrac{(\beta-\alpha)^2}{12}}$.
Raw Moments of Uniform Distribution
The $r^{th}$ raw moment of uniform distribution is
$$ \begin{equation*} \mu_r^\prime = \frac{\beta^{r+1}-\alpha^{r+1}}{(r+1)(\beta-\alpha)} \end{equation*} $$
Proof
The $r^{th}$ raw moment of uniform random variable $X$ is
$$ \begin{eqnarray*} \mu_r^\prime &=& E(X^r) \\ &=& \frac{1}{\beta-\alpha}\int_{\alpha}^\beta x^r\; dx\\ &=& \frac{1}{\beta-\alpha}\bigg[\frac{x^{r+1}}{r+1}\bigg]_\alpha^\beta\\ &=& \frac{\beta^{r+1}-\alpha^{r+1}}{(r+1)(\beta-\alpha)} \end{eqnarray*} $$
Mean deviation about mean of Uniform Distribution
The mean deviation about mean of Uniform Distribution is
$$ \begin{equation*} E[|X-\mu_1^\prime|] = \frac{\beta-\alpha}{4}. \end{equation*} $$
Proof
The mean deviation about mean of uniform distribution is
$$ \begin{eqnarray*} E[|X-\mu_1^\prime|] &=& E\big[|X-\frac{\alpha+\beta}{2}|\big] \\ &=& \frac{1}{\beta-\alpha}\int_{\alpha}^\beta \bigg(|x-\frac{\alpha+\beta}{2}|\bigg)\; dx \end{eqnarray*} $$
Let $t=x-\frac{\alpha+\beta}{2}$ $\Rightarrow dt = dx$ and as $x\to \beta $, $t\to -\frac{\beta-\alpha}{2}$ and as $x\to \alpha$, $t\to \frac{\beta-\alpha}{2}$.
Hence,
$$ \begin{eqnarray*} E[|X-\mu_1^\prime|] &=& \frac{1}{\beta-\alpha}\int_{-(\beta-\alpha)/2}^{(\beta-\alpha)/2} |t|\;dt\\ &=& \frac{2}{\beta-\alpha}\int_{0}^{(\beta-\alpha)/2} t\;dt\\ &=& \frac{2}{\beta-\alpha}\bigg(\frac{t^2}{2}\bigg)_{0}^{(\beta-\alpha)/2}\\ &=&\frac{(\beta-\alpha)^2}{4(\beta-\alpha)}\\ &=& \frac{\beta-\alpha}{4}. \end{eqnarray*} $$
M.G.F. of Uniform Distribution
The moment generating function of uniform distribution for $t\in R$ is
$$ \begin{equation*} M_X(t) = \frac{e^{t\beta}-e^{t\alpha}}{t(\beta-\alpha)},\; t\neq 0. \end{equation*} $$
Proof
Using the definition of moment generating function,the M.G.F. of $X$ is
$$ \begin{eqnarray*} M_X(t) &=& E(e^{tX}) \\ &=& \frac{1}{\beta-\alpha}\int_\alpha^\beta e^{tx} \; dx\\ &=& \frac{1}{\beta-\alpha}\bigg[\frac{e^{tx}}{t}\bigg]_\alpha^\beta \; dx\\ &=& \frac{1}{\beta-\alpha}\bigg[\frac{e^{t\beta}-e^{t\alpha}}{t}\bigg]\\ &=& \frac{e^{t\beta}-e^{t\alpha}}{t(\beta-\alpha)}. \end{eqnarray*} $$
Characteristics function of Uniform Distribution
The characteristics function of uniform distribution for $t\in R$ is
$$ \begin{equation*} \phi_X(t) = \frac{e^{it\beta}-e^{it\alpha}}{it(\beta-\alpha)},\; t\neq 0. \end{equation*} $$
Proof
Using the definition of characteristics function, the characteristics function of $X$ is
$$ \begin{eqnarray*} \phi_X(t) &=& E(e^{itX}) \\ &=& \frac{1}{\beta-\alpha}\int_\alpha^\beta e^{itx} \; dx\\ &=& \frac{1}{\beta-\alpha}\bigg[\frac{e^{itx}}{it}\bigg]_\alpha^\beta \; dx\\ &=& \frac{1}{\beta-\alpha}\bigg[\frac{e^{it\beta}-e^{it\alpha}}{it}\bigg]\\ &=& \frac{e^{it\beta}-e^{it\alpha}}{it(\beta-\alpha)}. \end{eqnarray*} $$
