Gamma Distribution
Gamma distribution is used to model a continuous random variable which takes positive values. Gamma distribution is widely used in science and engineering to model a skewed distribution.
In this tutorial, we are going to discuss various important statistical properties of gamma distribution like graph of gamma distribution for various parameter combination, derivation of mean, variance, harmonic mean, mode, moment generating function and cumulant generating function.
Gamma Distribution Definition
A continuous random variable $X$ is said to have an gamma distribution with parameters $\alpha$ and $\beta$ if its p.d.f. is given by
$$ \begin{align*} f(x)&= \begin{cases} \frac{1}{\beta^\alpha\Gamma(\alpha)}x^{\alpha -1}e^{-x/\beta}, & x > 0;\alpha, \beta > 0; \\ 0, & Otherwise. \end{cases} \end{align*} $$
where for $\alpha>0$, $\Gamma(\alpha)=\int_0^\infty x^{\alpha-1}e^{-x}; dx$ is called a gamma function.
Notation: $X\sim G(\alpha, \beta)$.
The parameter $\alpha$ is called the shape parameter and $\beta$ is called the scale parameter of gamma distribution.
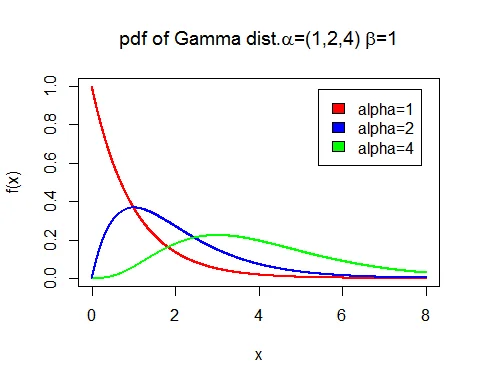
Graph of Gamma Distribution
Following is the graph of probability density function (pdf) of gamma distribution with parameter $\alpha=1$ and $\beta=1,2,4$.
Another form of gamma distribution
Another form of gamma distribution is
$$ \begin{equation*} f(x)=\left\{ \begin{array}{ll} \frac{1}{\alpha^\beta \Gamma(\beta)} x^{\beta -1}e^{-\frac{x}{\alpha}}, & \hbox{$x>0;\alpha, \beta >0$;} \\ 0, & \hbox{Otherwise.} \end{array} \right. \end{equation*} $$
Notation: $X\sim G(1/\alpha, \beta)$.
One parameter Gamma Distribution
Letting $\alpha=1$ in $G(\alpha, \beta)$, the probability density function of $X$ is as follows:
$$ \begin{equation*} f(x)=\left\{ \begin{array}{ll} \frac{1}{\Gamma(\beta)}x^{\beta -1}e^{-x}, & \hbox{$x>0;\beta >0$;} \\ 0, & \hbox{Otherwise.} \end{array} \right. \end{equation*} $$
which is one parameter gamma distribution.
Mean and Variance of Gamma Distribution
The mean of the gamma distribution $G(\alpha,\beta)$ is
$E(X)=\mu_1^\prime =\alpha\beta$.
Proof
The mean of $G(\alpha,\beta)$ distribution is
$$ \begin{eqnarray*} \text{mean = }\mu_1^\prime &=& E(X) \\ &=& \int_0^\infty x\frac{1}{\beta^\alpha\Gamma(\alpha)}x^{\alpha -1}e^{-x/\beta}\; dx\\ &=& \frac{1}{\beta^\alpha\Gamma(\alpha)}\int_0^\infty x^{\alpha+1 -1}e^{-x/\beta}\; dx\\ &=& \frac{1}{\beta^\alpha\Gamma(\alpha)}\Gamma(\alpha+1)\beta^{\alpha+1}\\ & & \quad (\text{Using }\int_0^\infty x^{n-1}e^{-x/\theta}\; dx = \Gamma(n)\theta^n )\\ &=& \alpha\beta,\;\quad (\because\Gamma(\alpha+1) = \alpha \Gamma(\alpha)) \end{eqnarray*} $$
Variance of Gamma distribution
The variance of gamma distribution $G(\alpha,\beta)$ is $\alpha\beta^2$.
Proof
The mean of gamma distribution $G(\alpha,\beta)$ is $\alpha\beta$.
To find variance of $X$, we need to find $E(X^2)$.
$$ \begin{eqnarray*} \mu_2^\prime&= &E(X^2)\\ &=& \int_0^\infty x^2\frac{1}{\beta^\alpha\Gamma(\alpha)}x^{\alpha -1}e^{-x/\beta}\; dx\\ &=& \frac{1}{\beta^\alpha\Gamma(\alpha)}\int_0^\infty x^{\alpha+2 -1}e^{-x/\beta}\; dx\\ &=& \frac{1}{\beta^\alpha\Gamma(\alpha)}\Gamma(\alpha+2)\beta^{\alpha+2}\\ & & \quad (\text{using gamma integral})\\ &=& \alpha(\alpha+1)\beta^2,\\ & & \quad (\because\Gamma(\alpha+2) = (\alpha+1) \alpha\Gamma(\alpha)) \end{eqnarray*} $$
Hence, the variance of gamma distribution is
$$ \begin{eqnarray*} \text{Variance = } \mu_2&=&\mu_2^\prime-(\mu_1^\prime)^2\\ &=&\alpha(\alpha+1)\beta^2 - (\alpha\beta)^2\\ &=&\alpha\beta^2(\alpha+1-\alpha)\\ &=&\alpha\beta^2. \end{eqnarray*} $$
Thus, variance of gamma distribution $G(\alpha,\beta)$ are $\mu_2 =\alpha\beta^2$.
Harmonic Mean of Gamma Distribution
Let $H$ be the harmonic mean of gamma distribution. Then the harmonic mean of $G(\alpha,\beta)$ distribution is $H=\beta(\alpha-1)$.
Proof
If $H$ is the harmonic mean of $G(\alpha,\beta)$ distribution then
$$ \begin{eqnarray*} \frac{1}{H}&=& E(1/X) \\ &=& \int_0^\infty \frac{1}{x}\frac{1}{\beta^\alpha\Gamma(\alpha)}x^{\alpha -1}e^{-x/\beta}\; dx\\ &=& \frac{1}{\beta^\alpha\Gamma(\alpha)}\int_0^\infty x^{\alpha-1 -1}e^{-x/\beta}\; dx\\ &=& \frac{1}{\beta^\alpha\Gamma(\alpha)}\Gamma(\alpha-1)\beta^{\alpha-1}\\ &=& \frac{1}{\beta^\alpha(\alpha-1)\Gamma(\alpha-1)}\Gamma(\alpha-1)\beta^{\alpha-1}\\ &=& \frac{1}{\beta(\alpha-1)}\\ & & \quad (\because\Gamma(\alpha) = (\alpha-1) \Gamma(\alpha-1)) \end{eqnarray*} $$
Therefore, harmonic mean of gamma distribution is
$$ \begin{equation*} H = \beta(\alpha-1). \end{equation*} $$
Mode of Gamma distribution
The mode of $G(\alpha,\beta)$ distribution is $\beta(\alpha-1)$.
Proof
The p.d.f. of gamma distribution with parameter $\alpha$ and $\beta$ is
$$ \begin{equation*} f(x) = \frac{1}{\beta^\alpha\Gamma(\alpha)}x^{\alpha -1}e^{-x/\beta},\; x > 0;\alpha, \beta > 0 \end{equation*} $$
Taking log of $f(x)$, we get
$$ \begin{equation*} \log f(x) = \log\bigg(\frac{1}{\beta^\alpha\Gamma(\alpha)}\bigg)+(\alpha-1)\log x -\frac{x}{\beta}. \end{equation*} $$
Differentiating $\log f(x)$ w.r.t. $x$ and equating to zero, we get
$$ \begin{eqnarray*} & & \frac{d\log f(x)}{dx}=0 \\ &\Rightarrow& 0+ \frac{\alpha-1}{x}-\frac{1}{\beta} =0\\ &\Rightarrow& x=\beta(\alpha-1). \end{eqnarray*} $$
Also,
$$ \begin{equation*} \frac{d^2\log f(x)}{dx^2}= -\frac{(\alpha-1)}{x^2}<0. \end{equation*} $$
Hence, the density $f(x)$ becomes maximum at $x =\beta(\alpha-1)$. Therefore, mode of gamma distribution is $\beta(\alpha-1)$.
Raw Moments of Gamma Distribution
The $r^{th}$ raw moment of gamma distribution is $\mu_r^\prime =\frac{\beta^r\Gamma(\alpha+r)}{\Gamma(\alpha)}$.
Proof
The $r^{th}$ raw moment of gamma distribution is
$$ \begin{eqnarray*} \mu_r^\prime &=& E(X^r) \\ &=& \int_0^\infty x^r\frac{1}{\beta^\alpha\Gamma(\alpha)}x^{\alpha -1}e^{-x/\beta}\; dx\\ &=& \frac{1}{\beta^\alpha\Gamma(\alpha)}\int_0^\infty x^{\alpha+r -1}e^{-x/\beta}\; dx\\ &=& \frac{1}{\beta^\alpha\Gamma(\alpha)}\Gamma(\alpha+r)\beta^{\alpha+r}\\ &=& \frac{\beta^r\Gamma(\alpha+r)}{\Gamma(\alpha)} \end{eqnarray*} $$
Thus, the $r^{th}$ raw moment of gamma distribution is $\mu_r^\prime =\frac{\beta^r\Gamma(\alpha+r)}{\Gamma(\alpha)}$.
M.G.F. of Gamma Distribution
The moment generating function of gamma distribution is $M_X(t) =\big(1-\beta t\big)^{-\alpha}$ for $t< \frac{1}{\beta}$.
Proof
The moment generating function of gamma distribution is
$$ \begin{eqnarray*} M_X(t) &=& E(e^{tX}) \\ &=& \int_0^\infty e^{tx}\frac{1}{\beta^\alpha\Gamma(\alpha)}x^{\alpha -1}e^{-x/\beta}\; dx\\ &=& \frac{1}{\beta^\alpha\Gamma(\alpha)}\int_0^\infty x^{\alpha -1}e^{-(1/\beta-t) x}\; dx\\ &=& \frac{1}{\beta^\alpha\Gamma(\alpha)}\frac{\Gamma(\alpha)}{\big(\frac{1}{\beta}-t\big)^\alpha}\\ &=& \frac{1}{\beta^\alpha}\frac{\beta^\alpha}{\big(1-\beta t\big)^\alpha}\\ &=& \big(1-\beta t\big)^{-\alpha}, \text{ (if $t<\frac{1}{\beta}$}) \end{eqnarray*} $$
Additive Property of Gamma Distribution
The sum of two independent Gamma variates is also Gamma variate.
Proof
Let $X_1$ and $X_2$ be two independent Gamma variate with parameters $(\alpha_1, \beta)$ and $(\alpha_2, \beta)$ respectively. Let $Y=X_1+X_2$. Then the m.g.f. of $Y$ is
$$ \begin{eqnarray*} M_Y(t) &=& E(e^{tY}) \\ &=& E(e^{t(X_1+X_2)}) \\ &=& E(e^{tX_1} e^{tX_2}) \\ &=& E(e^{tX_1})\cdot E(e^{tX_2})\\ & &\qquad (\because X_1, X_2 \text{ are independent })\\ &=& M_{X_1}(t)\cdot M_{X_2}(t)\\ &=& \big(1-\beta t\big)^{-\alpha_1}\cdot \big(1-\beta t\big)^{-\alpha_2}\\ &=& \big(1-\beta t\big)^{-(\alpha_1+\alpha_2)}. \end{eqnarray*} $$
which is the m.g.f. of Gamma variate with parameter $(\alpha_1+\alpha_2, \beta)$. Hence, by Uniqueness theorem of m.g.f. $Y=X_1+X_2$ is a Gamma variate with parameter $(\alpha_1+\alpha_2, \beta)$.
C.G.F. of Gamma Distribution
The cumulant generating function of gamma distribution is $K_X(t) =-\alpha \log \big(1-\beta t\big)$.
Proof
The cumulant generating function of gamma distribution is
$$ \begin{eqnarray*} K_X(t)& = & \log_e M_X(t)\\ &=& \log_e \big(1-\beta t\big)^{-\alpha}\\ &=&-\alpha \log \big(1-\beta t\big)\\ &=& \alpha\big(\beta t +\frac{\beta^2 t^2}{2}+\frac{\beta^3 t^3}{3}+\cdots +\frac{\beta^r t^r}{r}+\cdots\big)\\ & & \qquad (\because \log (1-a) = -(a+\frac{a^2}{2}+\frac{a^3}{3}+\cdots))\\ &=& \alpha\bigg(t\beta+\frac{t^2\beta^2}{2}+\cdots +\frac{t^r\beta^r (r-1)!}{r!}+\cdots\bigg)\\ \end{eqnarray*} $$
Thus the $r^{th}$ cumulant of gamma distribution is
$$ \begin{eqnarray*} k_r & =& \text{coefficient of } \frac{t^r}{r!}\text{ in } K_X(t)\\ &=& \alpha \beta^r(r-1)!, r=1,2,\cdots \end{eqnarray*} $$
Thus
$$ \begin{eqnarray*} k_1 &=& \alpha\beta =\mu_1^\prime \\ k_2 &=& \alpha\beta^2=\mu_2\\ k_3 &=& 2\alpha\beta^3=\mu_3\\ k_4 &=& 6\alpha\beta^4=\mu_4-3\mu_2^2\\ \Rightarrow \mu_4 &=& 3\alpha(2+\alpha)\beta^4. \end{eqnarray*} $$
The coefficient of skewness of gamma distribution is
$$ \begin{eqnarray*} \beta_1 &=& \frac{\mu_3^2}{\mu_2^3} \\ &=& \frac{(2\alpha\beta^3)^2}{(\alpha\beta^2)^3}\\ &=& \frac{4}{\alpha} \end{eqnarray*} $$
The coefficient of kurtosis of gamma distribution is
$$ \begin{eqnarray*} \beta_2 &=& \frac{\mu_4}{\mu_2^2} \\ &=& \frac{3\alpha(2+\alpha)\beta^4}{(\alpha\beta^2)^2}\\ &=& \frac{6+3\alpha}{\alpha} \end{eqnarray*} $$
It is clear from the $\beta_1$ coefficient of skewness and $\beta_2$ coefficient of kurtosis, that, as $\alpha\to \infty$, $\beta_1\to 0$ and $\beta_2\to 3$. Hence as $\alpha\to \infty$, gamma distribution tends to normal distribution.
For $\alpha =1$, gamma distribution $G(\alpha, \beta)$ becomes an exponential distribution with parameter $\beta$.
Conclusion
Hope you like Gamma Distribution article with step by step guide on various statistics properties of gamma probability. Use given below Gamma Distribution Calculator to calculate probabilities with solved examples.
