Normal Approximation to Binomial Distribution
Let $X$ be a binomially distributed random variable with number of trials $n$ and probability of success $p$.
The mean of $X$ is $\mu=E(X) = np$ and variance of $X$ is $\sigma^2=V(X)=np(1-p)$.
The general rule of thumb to use normal approximation to binomial distribution is that the sample size $n$ is sufficiently large if $np \geq 5$ and $n(1-p)\geq 5$.
For sufficiently large $n$, $X\sim N(\mu, \sigma^2)$. That is $Z=\frac{X-\mu}{\sigma}=\frac{X-np}{\sqrt{np(1-p)}} \sim N(0,1)$.
Formula
Continuity correction for normal approximation to binomial distribution are as follows:
- $P(X=A)=P(A-0.5<X<A+0.5)$
- $P(X<A)=P(X<A-0.5)$
- $P(X\leq A)=P(X<A+0.5)$
- $P(A< X\leq B)=P(A-0.5<X<B+0.5)$
- $P(A\leq X< B)=P(A-0.5<X<B-0.5)$
- $P(A\leq X\leq B)=P(A-0.5<X<B+0.5)$
Example
In a certain Binomial distribution with probability of success $p=0.20$ and number of trials $n = 30$.
Compute
a. the probability of getting 5 successes,
b. the probability of getting at least 5 successes,
c. the probability of getting between 5 and 10 (inclusive) successes.
Solution
Let $X$ denote the number of successes in 30 trials and let $p$ be the probability of success.
Given that $n =30$ and $p=0.2$. Thus $X\sim B(30, 0.2)$.
Here $n*p = 30\times 0.2 = 6>5$ and $n*(1-p) = 30\times (1-0.2) = 24>5$, we use Normal approximation to Binomial distribution.
Mean of $X$ is
$$ \begin{aligned} \mu&= n*p \\ &= 30 \times 0.2 \\ &= 6. \end{aligned} $$
and standard deviation of $X$ is
$$ \begin{aligned} \sigma &= \sqrt{n*p*(1-p)} \\ &= \sqrt{30 \times 0.2 \times (1- 0.2)}\\ &=2.1909. \end{aligned} $$
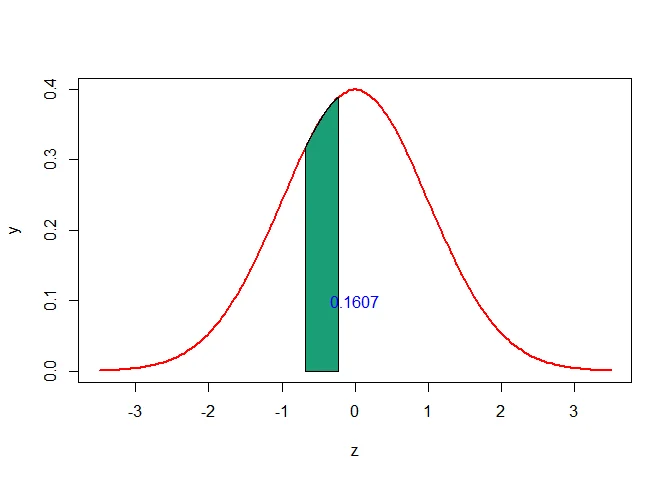
a. Using the continuity correction, $P(X=5)$ can be written as $P(5-0.5<X<5+0.5)=P(4.5<X<5.5)$.
The $Z$-scores that corresponds to $4.5$ and $5.5$ are
$$ \begin{aligned} z_1=\frac{4.5-\mu}{\sigma}=\frac{4.5-6}{2.1909}\approx-0.68 \end{aligned} $$
and
$$ \begin{aligned} z_2=\frac{5.5-\mu}{\sigma}=\frac{5.5-6}{2.1909}\approx-0.23 \end{aligned} $$
Thus the probability of getting exactly 5 successes is
$$ \begin{aligned} P(X= 5) & = P(4.5<X<5.5)\\ &=P(z_1< Z< z_2)\\ &=P(-0.68<Z<-0.23)\\ &=P(Z<-0.23)-P(Z<-0.68)\\ & = 0.409-0.2483\\ & = 0.1607 \end{aligned} $$
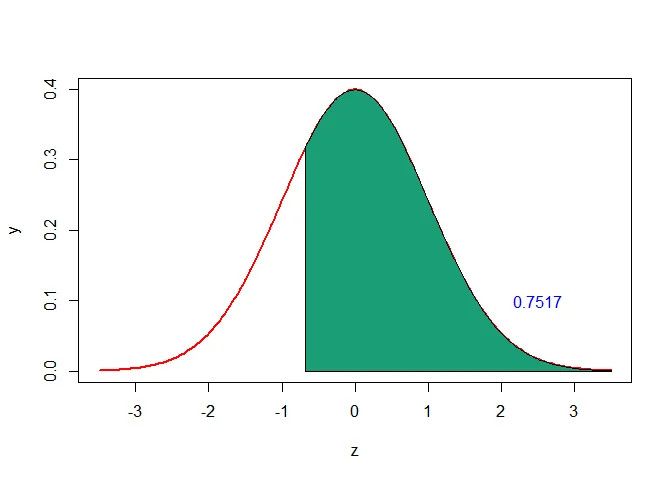
b. Using the continuity correction, the probability of getting at least 5 successes i.e., $P(X\geq 5)$ can be written as $P(X\geq5)=P(X\geq 5-0.5)=P(X\geq4.5)$.
The $Z$-score that corresponds to $4.5$ is
$$ \begin{aligned} z=\frac{4.5-\mu}{\sigma}=\frac{4.5-6}{2.1909}\approx-0.68 \end{aligned} $$
Thus, the probability of getting at least 5 successes is
$$ \begin{aligned} P(X\geq 5) &= P(X\geq4.5)\\ &= 1-P(X<4.5)\\ &= 1-P(Z<-0.68)\\ & = 1-0.2483\\ & = 0.7517 \end{aligned} $$
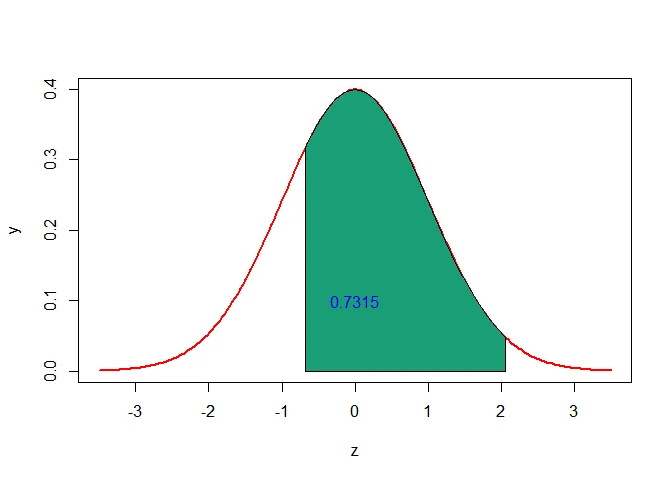
c. Using the continuity correction, the probability of getting between 5 and 10 (inclusive) successes is $P(5\leq X\leq 10)$ can be written as $P(5-0.5<X<10+0.5)=P(4.5<X<10.5)$.
The $Z$-scores that corresponds to $4.5$ and $10.5$ are respectively
$$ \begin{aligned} z_1=\frac{4.5-\mu}{\sigma}=\frac{4.5-6}{2.1909}\approx-0.68 \end{aligned} $$
and
$$ \begin{aligned} z_2=\frac{10.5-\mu}{\sigma}=\frac{10.5-6}{2.1909}\approx2.05 \end{aligned} $$
$$ \begin{aligned} P(5\leq X\leq 10) &= P(5-0.5 < X <10+0.5)\\ &= P(4.5 < X <10.5)\\ &=P(-0.68\leq Z\leq 2.05)\\ &=P(Z\leq 2.05)-P(Z\leq -0.68)\\ &=0.9798-0.2483\\ &=0.7315 \end{aligned} $$