Chi-square test for variance Calculator
In this tutorial we will discuss a method for testing a claim made about the population variance $\sigma^2$ or population standard deviation $\sigma$. To test the claim about the population variance or population standard deviation we use chi-square test.
Use this chi square test for variance calculator to calculate Chi square Test Statistics, degress of freedom,chi-square critical values and p vlaue using population standard deviation,sample size, sample size and deviation,level of significance and left/right or two tailed.
Chi-Square Test Calculator
| Chi-square test for variance calculator | |
|---|---|
| Population Standard Deviation ($\sigma$) | |
| Sample Size ($n$) | |
| Sample Standard Deviation ($s$) | |
| Level of Significance ($\alpha$) | |
| Tail : | Left tailed Right tailed Two tailed |
| Results | |
| Chi-square Test Statistics ($\chi^2$): | |
| Degrees of Freedom: | |
| $\chi^2$-critical value(s): | |
| p-value: | |
How to use Chi-Square test for variances calculator?
Step 1 - Enter the Population standard deviation
Step 2 - Enter the sample size
Step 3 - Enter the sample Standard Deviation
Step 4 - Enter the level of Significance ($\alpha$)
Step 5 - Select the left tailed or right tailed or two tailed for chi-square test
Step 6 - Click on “Calculate” button to calculate chi square for variance
Step 7 - Calculate Test Statistics ($\chi^2$)
Step 8 - Calculate Degrees of Freedom
Step 9 - Calculate chi square test critical value
Step 10 - Calculate chi square test p value
Chi-Square Test Formula
The test statistic under the null hypothesis $H_0$ is
$$ \chi^2_{obs} = \frac{(n-1)s^2}{\sigma^2_0} $$
where,
$s^2 =\dfrac{1}{n-1} \sum (x_i -\overline{x})^2$is the sample variance.
The test statistic follows chi-square distribution with $n-1$ degrees of freedom.
Chi-square Test for the Variance
Let $X_1, X_2, \cdots, X_n$ be a random sample from a normal population with mean $\mu$ and variance $\sigma^2$.
Let $\overline{x}=\frac{1}{n} \sum x_i$ be the sample mean and $s^2=\frac{1}{n-1} \sum (x_i-\overline{x})^2$ be the sample variance.
Assumptions
a. The sample must be randomly selected from the population.
b. The population must be normally distribution for the variable under study.
c. The observations must be independent.
Step by Step Procedure
We wish to test the null hypothesis $H_0 : \sigma^2 = \sigma^2_0$, where $\sigma^2_0$ is the specified value of the population variance.
Step 1 State the hypothesis testing problem
The hypothesis testing problem can be structured in any one of the three situations as follows:
| Situation | Hypothesis Testing Problem |
|---|---|
| Situation A : | $H_0: \sigma^2=\sigma^2_0$ against $H_a : \sigma^2 < \sigma^2_0$ (Left-tailed) |
| Situation B : | $H_0: \sigma^2=\sigma^2_0$ against $H_a : \sigma^2 > \sigma^2_0$ (Right-tailed) |
| Situation C : | $H_0: \sigma^2=\sigma^2_0$ against $H_a : \sigma^2 \neq \sigma^2_0$ (Two-tailed) |
Step 2 Define the test statistic
The** test statistic** for testing above hypothesis is
$$ \chi^2 =\frac{(n-1)s^2}{\sigma^2} $$
The test statistic chi-square follows chi-square ($\chi^2$) distribution with $n-1$ degrees of freedom.
Step 3 Specify the level of significance $\alpha$
Step 4 Determine the critical values
For the specified value of $\alpha$ determine the critical region depending upon the alternative hypothesis.
- For left-tailed alternative hypothesis: Find the $\chi^2$-critical value using
$$ P(\chi^2\leq \chi^2 _{1-\alpha,n-1}) = \alpha. $$
- For right-tailed alternative hypothesis: $\chi^2_\alpha$.
$$ P(\chi^2\geq\chi^2_{\alpha, n-1}) = \alpha. $$
- For two-tailed alternative hypothesis: $\chi^2_{\alpha/2}$.
$$ P(\chi^2\leq \chi^2 _{1-\alpha/2,n-1} \text{ or } \chi^2\geq \chi^2_{\alpha/2,n-1}) = \alpha. $$
Step 5 Computation
Compute the test statistic under the null hypothesis $H_0$ using
$$ \chi^2_{obs} = \frac{(n-1)s^2}{\sigma^2_0} $$
Step 6 Decision (Traditional Approach)
Based on the critical values.
- For left-tailed alternative hypothesis: Reject $H_0$ if
$\chi^2_{obs}\leq \chi^2_{1-\alpha,n-1}$. - For right-tailed alternative hypothesis: Reject $H_0$ if
$\chi^2_{obs}\geq \chi^2_{\alpha,n-1}$. - For two-tailed alternative hypothesis: Reject $H_0$ if
$\chi^2_{obs}\leq \chi^2_{1-\alpha/2, n-1}$or$\chi^2_{obs}\geq \chi^2_{\alpha/2, n-1}$.
OR
Step 6 Decision ($p$-value Approach)
It is based on the $p$-value.
| Alternative Hypothesis | Type of Hypothesis | $p$-value |
|---|---|---|
| $H_a: \sigma^2<\sigma^2_0$ | Left-tailed | $p$-value $= P(\chi^2\leq \chi^2_{obs})$ |
| $H_a: \sigma^2>\sigma^2_0$ | Right-tailed | $p$-value $= P(\chi^2\geq \chi^2_{obs})$ |
| $H_a: \sigma^2\neq \sigma^2_0$ | Two-tailed | $p$-value $= 2P(\chi^2\geq \chi^2_{obs})$ |
If $p$-value is less than $\alpha$, then reject the null hypothesis $H_0$ at $\alpha$ level of significance, otherwise fail to reject $H_0$ at $\alpha$ level of significance.
In this tutorial we will discuss some numerical examples based on chi-square test for variance.
Example 1 - Chi-Square Test for Variance
A statistician wishes to test the claim that the standard deviation of the weights of firemen is less than 25 pounds. She selected a random sample of 20 firemen and found $s = 23.2$ pounds. Assuming that the weights of firemen are normally distributed, test the claim of the statistician at the 0.05 level of significance.
Solution
Given that the sample size $n = 20$ and sample standard deviation $s = 23.2$.
Step 1 Hypothesis Problem
The hypothesis testing problem is $H_0 : \sigma = 25$ against $H_1 : \sigma < 25$ ($\text{left-tailed}$).
Step 2 Test Statistic
The test statistic for testing above hypothesis testing problem is
$$ \chi^2 =\frac{(n-1)s^2}{\sigma^2} $$
The test statistic follows a chi-square distribution with $n-1$ degrees of freedom.
Step 3 Level of Significance
The significance level is $\alpha = 0.05$.
Step 4 Critical Value
As the alternative hypothesis is $\text{left-tailed}$, the chi-square ($\chi^2$) critical value for $\alpha=0.05$ level of significance and $n-1 = 19$ degrees of freedom $\text{ is }$ $\text{10.117}$ (from $\chi^2$ statistical table).
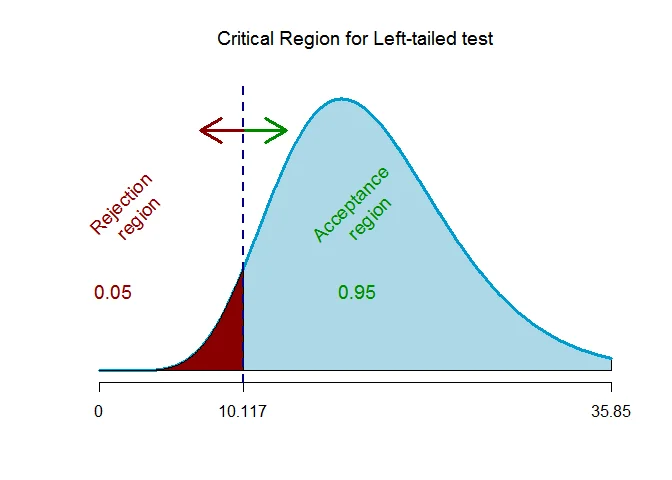
The rejection region (i.e. critical region) is $\chi^2 < 10.117$.
Step 5 Test Statistic
The test statistic under the null hypothesis is
$$ \begin{aligned} \chi^2 &=\frac{(n-1)s^2}{\sigma^2_0}\\ &= \frac{(20-1)*(23.2)^2}{(25)^2}\\ &= 16.362 \end{aligned} $$
Step 6 Decision (Traditional approach)
The test statistic is chi-square ($\chi^2) =16.362$ which falls $outside$ the critical region, we $\text{fail to reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value Approach)
This is a $\text{left-tailed}$ test, so the p-value is the area to the left of the test statistic ($\chi^2=16.362$) is p-value = $0.367$.
The p-value is $0.367$ which is $\text{greater than}$ the significance level of $\alpha = 0.05$, we $\text{fail to reject}$ the null hypothesis.
Example 2 - Chi Square Test Calculator
An engineer is investing the amount of standard deviation in the time it takes a 3D printer to make a particular part. The engineer believes that the standard deviation in the time it takes to make the part is more than 2. Test this at $\alpha = 0.01$ level of significance, using 11 sample times taken while the printer was making these parts. The sample standard deviation is 2.3.
Solution
Given that the sample size $n = 11$ and sample standard deviation $s = 2.3$.
Step 1 Hypothesis Problem
The hypothesis testing problem is $H_0 : \sigma = 2$ against $H_1 : \sigma > 2$ ($\text{right-tailed}$)
Step 2 Test Statistic
The test statistic for testing above hypothesis testing problem is
$$ \chi^2 =\frac{(n-1)s^2}{\sigma^2} $$
The test statistic follows chi-square distribution with $n-1$ degrees of freedom.
Step 3 Level of Significance
The significance level is $\alpha = 0.01$.
Step 4 Critical Value
As the alternative hypothesis is $\text{right-tailed}$, the chi-square ($\chi^2$ ) critical value for $\alpha=0.01$ level of significance and $n-1 = 10$ degrees of freedom $\text{ is }$ $\text{23.209}$ (from $\chi^2$ statistical table).
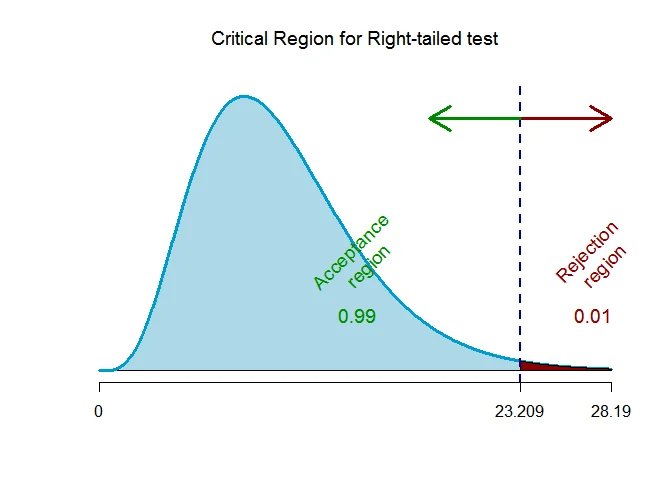
The rejection region (i.e. critical region) is $\chi^2 > 23.209$.
Step 5 Test Statistic
The test statistic under the null hypothesis is
$$ \begin{aligned} \chi^2& =\frac{(n-1)s^2}{\sigma^2_0}\\ &= \frac{(11-1)*(2.3)^2}{(2)^2}\\ &= 13.225 \end{aligned} $$
Step 6 Decision (Traditional approach)
The test statistic is $\chi^2 =13.225$ which falls $outside$ the critical region, we $\text{fail to reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value Approach)
This is a $\text{right-tailed}$ test, so the p-value is the area to the left of the test statistic ($\chi^2=13.225$) is p-value = $0.2114$.
The p-value is $0.2114$ which is $\text{greater than}$ the significance level of $\alpha = 0.01$, we $\text{fail to reject}$ the null hypothesis.
Example 3 Chi Square Test Variance Calculator
A cigarette manufacturer wishes to test the claim that the variance of nicotine content of its cigarettes is 0.644. Nicotine content is measured in milligrams and is assumed normally distributed. A sample of 20 cigarettes has a standard deviation of 1.00 milligram. At $\alpha = 0.01$, is there enough evidence to reject the manufacturer’s claim?
Solution
Given that the sample size $n = 20$ and sample standard deviation $s = 1$.
Step 1 Hypothesis Problem
The hypothesis testing problem is $H_0 : \sigma^2 = 0.644$ against $H_1 : \sigma^2 \neq 0.644$ ($\text{two-tailed}$)
Step 2 Test Statistic
The test statistic for testing above hypothesis testing problem is
$$ \chi^2 =\frac{(n-1)s^2}{\sigma^2} $$
The test statistic follows chi-square distribution with $n-1$ degrees of freedom.
Step 3 Level of Significance
The significance level is $\alpha = 0.01$.
Step 4 Critical Value
As the alternative hypothesis is $\text{two-tailed}$, the chi-square ($\chi^2$) critical values for $\alpha=0.01$ level of significance and $n-1 = 19$ degrees of freedom $\text{ are }$ $\text{6.844 and 38.582}$ (from $\chi^2$ statistical table).
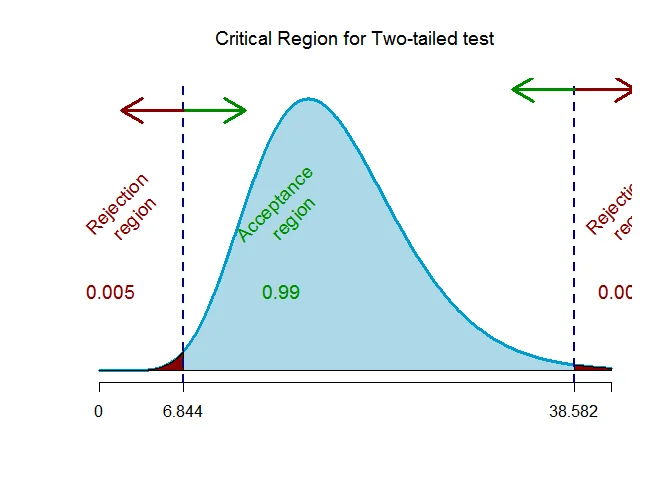
The rejection region (i.e. critical region) is $\chi^2 < 6.844$ or $\chi^2 > 38.582$.
Step 5 Test Statistic
The test statistic under the null hypothesis is
$$ \begin{aligned} \chi^2 &=\frac{(n-1)s^2}{\sigma^2_0}\\ &= \frac{(20-1)*(1)^2}{(0.8024961)^2}\\ &= 29.503 \end{aligned} $$
Step 6 Decision (Traditional approach)
The test statistic is $\chi^2 =29.503$ which falls $outside$ the critical region, we $\text{fail to reject}$ the null hypothesis.
OR
Step 6 Decision ($p$-value Approach)
This is a $\text{two-tailed}$ test, so the p-value is the area to the left of the test statistic ($\chi^2=29.503$) is p-value = $0.0585$.
The p-value is $0.0585$ which is $\text{greater than}$ the significance level of $\alpha = 0.01$, we $\text{fail to reject}$ the null hypothesis.
Conclusion
Hope you like Chi-Square Test for Variance Calculator and step by step guide with examples and calculator.
You can read more about F-Test for two variance calculator to calculate f test and critical values and Paired t test calculator to calculate paired t test statistics and critical values.
Read more about other Statistics Calculator on below links
- Descriptive Statistics Calculators
- Hypothesis Testing Calculators
- Probability Distribution
- Confidence Interval Calculators
- Correlation Regression Calculators
- Probability Theory Calculators
- Sample Size and Power Calculators
